
【题目】(1)已知:如图1,在△ABC中,∠ABC的平分线与∠ACB的平分线交于点O,求证:∠BOC=90°+![]() ∠A;
∠A;
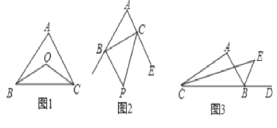
(2)如图2,在△ABC中,BP,CP分别是△ABC的外角∠DBC和∠ECB的平分线,试探究∠BPC与∠A的关系.
(3)如图3,在△ABC中,CE平分∠ACB,BE是△ABC的外角∠ABD的平分线,试探究∠BEC与∠A的关系.
【答案】(1)见解析;(2)∠BPC=90°![]() ∠A,理由见解析;(3)2∠BEC=∠A.
∠A,理由见解析;(3)2∠BEC=∠A.
【解析】
(1)先根据三角形内角和定理得到∠BOC=180°-∠OBC-∠OCB,则2∠BOC=360°-2∠OBC-2∠OCB,再根据角平分线的定义得∠ABC=2∠OBC,∠ACB=2∠OCB,则2∠BOC=360°-∠ABC-∠ACB,易得∠BOC=90°+![]() ∠A;
∠A;
(2)根据三角形外角平分线的性质可得∠BCP=![]() (∠A+∠ABC)、∠PBC=
(∠A+∠ABC)、∠PBC=![]() (∠A+∠ACB);根据三角形内角和定理可得∠BPC=90°-
(∠A+∠ACB);根据三角形内角和定理可得∠BPC=90°-![]() ∠A;
∠A;
(3)根据CE为∠ABC的角平分线,BE为△ABC外角∠ABD的平分线,可知,∠A=180°-∠1-∠3,∠E=180°-∠4-∠ABE=180°-∠3-![]() (∠A+2∠1),两式联立可得2∠BEC=∠A.
(∠A+2∠1),两式联立可得2∠BEC=∠A.
(1)证明:在△BOC中,
∵∠BOC=180°∠OBC∠OCB,
∴2∠BOC=360°2∠OBC2∠OCB,
∵BO平分∠ABC,CO平分∠ACB,
∴∠ABC=2∠OBC,∠ACB=2∠OCB,
∴2∠BOC=360°(∠ABC+∠ACB),
∵∠ABC+∠ACB=180°∠A,
∴2∠BOC=180°+∠A,
∴∠BOC=90°+![]() ∠A;
∠A;
(2)∠BPC=90°![]() ∠A.
∠A.
证明:∵BP、CP为△ABC两外角∠ABC、∠ACB的平分线,∠A为x°,
∴∠BCP=![]() (∠A+∠ABC)、∠PBC=
(∠A+∠ABC)、∠PBC=![]() (∠A+∠ACB),
(∠A+∠ACB),
由三角形内角和定理得,∠BPC=180°∠BCP∠PBC=180°![]() [∠A+(∠A+∠ABC+∠ACB)]=180°
[∠A+(∠A+∠ABC+∠ACB)]=180°![]() (∠A+180°)=90°
(∠A+180°)=90°![]() ∠A;
∠A;
(3)2∠BEC=∠A.
证明:∵CE为∠ACB的角平分线,BE为△ABC外角∠ABD的平分线,两角平分线交于点E,
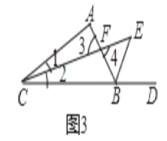
∴∠1=∠2,∠ABE=![]() (∠A+2∠1),∠3=∠4,
(∠A+2∠1),∠3=∠4,
在△ACF中,∠A=180°∠1∠3
∴∠1+∠3=180°∠A①
在△BEF中,∠E=180°∠4∠ABE=180°∠3![]() (∠A+2∠1),
(∠A+2∠1),
即2∠E=360°2∠3∠A2∠1=360°2(∠1+∠3)∠A②,
把①代入②得2∠E=∠A,即2∠BEC=∠A.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象相交于点A(﹣2,1),点B(1,n).
的图象相交于点A(﹣2,1),点B(1,n).
(1)求此一次函数和反比例函数的解析式;
(2)请直接写出满足不等式kx+b﹣![]() <0的解集;
<0的解集;
(3)在平面直角坐标系的第二象限内边长为1的正方形EFDG的边均平行于坐标轴,若点E(﹣a,a),如图,当曲线y= ![]() (x<0)与此正方形的边有交点时,求a的取值范围.
(x<0)与此正方形的边有交点时,求a的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】西安市阳光酸奶厂,每天生产A,B两种酸奶共800箱.A、B两种酸奶的成本和利润如下表.设每天生产A种酸奶x箱,两种酸奶共获利y元.

(1)请写出y关于x的函数关系式
(2)如果该酸奶厂每天至少投入成本48000元,那么每天最多获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
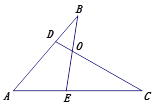
【题目】如图,点D在AB上,点E在AC上,BE、CD相交于点O.
(1)若∠A=50°,∠BOD=70°,∠C=30°,求∠B的度数;
(2)试猜想∠BOC与∠A+∠B+∠C之间的关系,并证明你猜想的正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
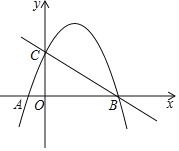
【题目】抛物线![]() 经过点A(-1,0)、B(4,0),与y轴交于点C(0,4).
经过点A(-1,0)、B(4,0),与y轴交于点C(0,4).
(1)求抛物线的表达式;
(2)点P为直线BC上方抛物线的一点,分别连接PB、PC,若直线BC恰好平分四边形COBP的面积,求P点坐标;
(3)在(2)的条件下,是否在该抛物线上存在一点Q,该抛物线对称轴上存在一点N,使得以A、P、Q、N为顶点的四边形为平行四边形?若存在,求出Q点坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
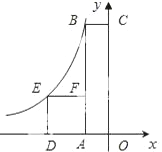
【题目】如图,四边形OABC是矩形,四边形ADEF是正方形,点A、D在x轴的负半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数![]() 的图象上,正方形ADEF的面积为4,且BF=2AF,则k值为________.
的图象上,正方形ADEF的面积为4,且BF=2AF,则k值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
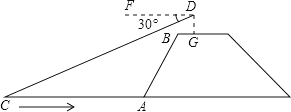
【题目】如图,兰兰站在河岸上的G点,看见河里有一只小船沿垂直于岸边的方向划过来,此时,测得小船C的俯角是∠FDC=30°,若兰兰的眼睛与地面的距离是1.5米,BG=1米,BG平行于AC所在的直线,迎水坡的坡度i=4:3,坡长AB=10米,求小船C到岸边的距离CA的长?(参考数据:![]() =1.73,结果保留两位有效数字)
=1.73,结果保留两位有效数字)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com