
【题目】直线y=-kx+k-3与直线y=kx在同一坐标系中的大致图象可能是( )
A. 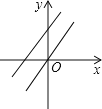 B.
B. 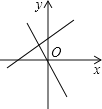 C.
C. 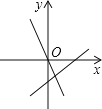 D.
D. 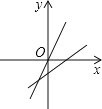
【答案】B
【解析】若y=kx过第一、三象限,则k>0,所以y=-kx+k-3过第二、四象限,可对A、D进行判断;若y=kx过第二、四象限,则k<0,-k>0,k-3<0,所以y=-kx+k-3过第一、三象限,与y轴的交点在x轴下方,则可对B、C进行判断.
A、y=kx过第一、三象限,则k>0,所以y=-kx+k-3过第二、四象限,所以A选项错误;
B、y=kx过第二、四象限,则k<0,-k>0,k-3<0,所以y=-kx+k-3过第一、三象限,与y轴的交点在x轴下方,所以B选项正确;
C、y=kx过第二、四象限,则k<0,-k>0,k-3<0,所以y=-kx+k-3过第一、三象限,与y轴的交点在x轴下方,所以C选项错误;
D、y=kx过第一、三象限,则k>0,所以y=-kx+k-3过第二、四象限,所以D选项错误.
故选:B.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
【题目】在数轴上,把表示数![]() 的点称为基准点,记作点
的点称为基准点,记作点![]() .对于两个不同的点
.对于两个不同的点![]() 和
和![]() ,若点
,若点![]() 、点
、点![]() 到点
到点![]() 的距离相等,则称点
的距离相等,则称点![]() 和点
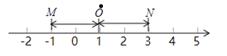
和点![]() 互为基准变换点.例如:下图中,点
互为基准变换点.例如:下图中,点![]() 表示数
表示数![]() ,点N表示数
,点N表示数![]() ,它们与基准点
,它们与基准点![]() 的距离都是
的距离都是![]() 个单位长度,点
个单位长度,点![]() 与点
与点![]() 互为基准变换点.
互为基准变换点.
(1)已知点![]() 表示数
表示数![]() ,点
,点![]() 表示数
表示数![]() ,点
,点![]() 与点
与点![]() 互为基准变换点.
互为基准变换点.
①若![]() ,则
,则![]() _______ ;
_______ ;
②用含![]() 的式子表示
的式子表示![]() ,则
,则![]() _____;
_____;
(2)对点![]() 进行如下操作:先把点
进行如下操作:先把点![]() 表示的数乘以
表示的数乘以![]() ,再把所得数表示的点沿着数轴向左移动
,再把所得数表示的点沿着数轴向左移动![]() 个单位长度得到点
个单位长度得到点![]() .若点
.若点![]() 与点
与点![]() 互为基准变换点,则点
互为基准变换点,则点![]() 表示的数是_____________;
表示的数是_____________;
(3)点![]() 在点
在点![]() 的左边,点
的左边,点![]() 与点
与点![]() 之间的距离为
之间的距离为![]() 个单位长度.对
个单位长度.对![]() 、
、![]() 两点做如下操作:点
两点做如下操作:点![]() 沿数轴向右移动
沿数轴向右移动![]() 个单位长度得到
个单位长度得到![]() ,
,![]() 为
为![]() 的基准变换点,点
的基准变换点,点![]() 沿数轴向右移动
沿数轴向右移动![]() 个单位长度得到
个单位长度得到![]() ,
,![]() 为
为![]() 的基准变换点,……,依此顺序不断地重复,得到
的基准变换点,……,依此顺序不断地重复,得到![]() ,
,![]() ,…,
,…,![]() .
.![]() 为
为![]() 的基准变换点,将数轴沿原点对折后
的基准变换点,将数轴沿原点对折后![]() 的落点为
的落点为![]() ,
,![]() 为
为![]() 的基准变换点,将数轴沿原点对折后
的基准变换点,将数轴沿原点对折后![]() 的落点为
的落点为![]() ,……,依此顺序不断地重复,得到
,……,依此顺序不断地重复,得到![]() ,
,![]() ,…,
,…,![]() .若无论
.若无论![]() 为何值,
为何值,![]() 与
与![]() 两点间的距离都是
两点间的距离都是![]() ,则
,则![]() _________.
_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正整数 1 至 2024 按一定规律排列成如图所示的 8 列,规定从上到下依次为第 1 行,第 2 行,第 3 行,…从左往右依次为第 1 列至第 8 列.
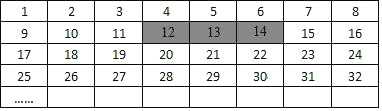
(1)数 56 在第 行 列 ;
(2)平移图中带阴影的方框,使方框框住相邻的三个数,若被框住的三个数中最大的一个数为 x,则被框的三个数的和能否等于 2019?若能,请求出 x;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了给游客提供更好的服务,某景区随机对部分游客进行了关于“景区服务工作满意度”的调查,并根据调查结果绘制成如下不完整的统计图表.
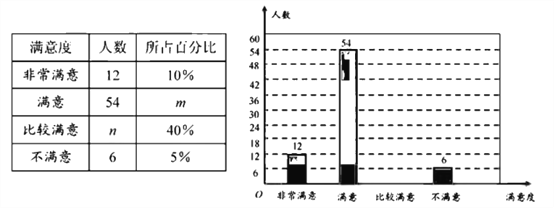
根据图表信息,解答下列问题:
(1)本次调查的总人数为 ,表中![]() 的值为 ;
的值为 ;
(2)请补全条形统计图;
(3)据统计,该景区平均每天接待游客约3600人,若将“非常满意”和“满意”作为游客对景区服务工作的肯定,请你估计该景区服务工作平均每天得到多少名游客的肯定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知:如图1,在△ABC中,∠ABC的平分线与∠ACB的平分线交于点O,求证:∠BOC=90°+![]() ∠A;
∠A;
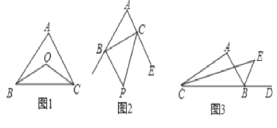
(2)如图2,在△ABC中,BP,CP分别是△ABC的外角∠DBC和∠ECB的平分线,试探究∠BPC与∠A的关系.
(3)如图3,在△ABC中,CE平分∠ACB,BE是△ABC的外角∠ABD的平分线,试探究∠BEC与∠A的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是45°,向前走6m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°.
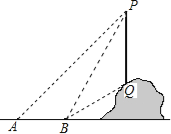
(1)求∠BPQ的度数;
(2)求该电线杆PQ的高度(结果精确到1m).
备用数据:![]() ,
,![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AM∥BN,∠A=60°,点P是射线AM上一动点(不与点A重合).BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
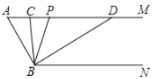
(发现)
(1)∵AM∥BN,∴∠ACB=_______;(填相等的角)
(2)求∠ABN、∠CBD的度数;
解:∵AM∥BN,
∴∠ABN+∠A=180°,
∵∠A=60°,
∴∠ABN=∠ABP+∠PBN=______,
∵BC平分∠ABP,BD平分∠PBN,
∴∠ABP=2∠CBP,∠PBN=______,
∴2∠CBP+2∠DBP=120°,
∴∠CBD=∠CBP+∠DBP=______.
(操作)
(3)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com