
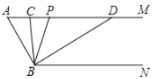
【题目】如图,已知AM∥BN,∠A=60°,点P是射线AM上一动点(不与点A重合).BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(发现)
(1)∵AM∥BN,∴∠ACB=_______;(填相等的角)
(2)求∠ABN、∠CBD的度数;
解:∵AM∥BN,
∴∠ABN+∠A=180°,
∵∠A=60°,
∴∠ABN=∠ABP+∠PBN=______,
∵BC平分∠ABP,BD平分∠PBN,
∴∠ABP=2∠CBP,∠PBN=______,
∴2∠CBP+2∠DBP=120°,
∴∠CBD=∠CBP+∠DBP=______.
(操作)
(3)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
【答案】(1) ![]() ;(2)120°,
;(2)120°,![]() ,60°;(3)不变,
,60°;(3)不变,![]() ,理由见解析.
,理由见解析.
【解析】
(1)由平行线的性质:两直线平行,内错角相等即可得;
(2)根据平行线的性质及角平分线的定义即可;
(3)由平行线的性质及角平分线的定义即可.
解:(1)∵AM∥BN,
∴∠ACB=![]() ;
;
故答案为:![]()
(2)∵AM∥BN
∴∠ABN+∠A=180°,
∵∠A=60°,
∴∠ABN=120°,
∴∠ABP+∠PBN=120°,
∵BC平分∠ABP,BD平分∠PBN,
∴∠ABP=2∠CBP,∠PBN=2∠PBD,
∴2∠CBP+2∠DBP=120°,
∴∠CBD=∠CBP+∠DBP=60°.
故答案为:120°、![]() 、60°
、60°
(3)不变,![]() ,
,
理由:![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
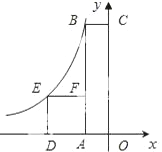
【题目】如图,四边形OABC是矩形,四边形ADEF是正方形,点A、D在x轴的负半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数![]() 的图象上,正方形ADEF的面积为4,且BF=2AF,则k值为________.
的图象上,正方形ADEF的面积为4,且BF=2AF,则k值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
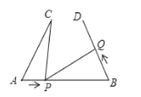
【题目】如图,AB=6cm,AC=BD=4cm.∠CAB=∠DBA=60 ,点 P 在线段 AB 上以 1cm/s 的速度由点A 向点 B 运动,同时,点 Q 在线段 BD 上由点 B 向点 D 运动。它们运动的时间为 t(s),则点 Q的运动速度为________cm/s,使得 A. C. P 三点构成的三角形与 B. P、Q 三点构成的三角形全等。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C是线段AB的中点,延长线段AB至点D,使BD=AB,延长AD至点E,使DE=AC.
![]()
(1)依题意画出图形(尺规作图),则![]() =_________(直接写出结果);
=_________(直接写出结果);
(2)若DE=3,求AB的长;
(3)请写出与BE长度相同的线段.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,AB=2,∠C=60°,我们把菱形ABCD的对称中心O称作菱形的中心.菱形ABCD在直线l上向右作无滑动的翻滚,每绕着一个顶点旋转60°叫一次操作,则经过1次这样的操作菱形中心O所经过的路径长为 ;经过3n(n为正整数)次这样的操作菱形中心O所经过的路径总长为 .(结果都保留π)

查看答案和解析>>
科目:初中数学 来源: 题型:
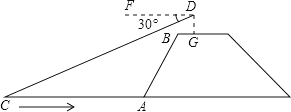
【题目】如图,兰兰站在河岸上的G点,看见河里有一只小船沿垂直于岸边的方向划过来,此时,测得小船C的俯角是∠FDC=30°,若兰兰的眼睛与地面的距离是1.5米,BG=1米,BG平行于AC所在的直线,迎水坡的坡度i=4:3,坡长AB=10米,求小船C到岸边的距离CA的长?(参考数据:![]() =1.73,结果保留两位有效数字)
=1.73,结果保留两位有效数字)
查看答案和解析>>
科目:初中数学 来源: 题型:
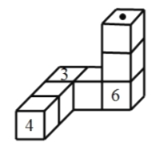
【题目】如图,每个立方体的![]() 个面上分别写有
个面上分别写有![]() 到
到![]() 这
这![]() 个自然数,并且任意两个相对面上所写两个数字之和为
个自然数,并且任意两个相对面上所写两个数字之和为![]() ,把这样的
,把这样的![]() 个立方体一个挨着一个地连接起来,紧挨着两个面上的数字之和为
个立方体一个挨着一个地连接起来,紧挨着两个面上的数字之和为![]() ,则图中“· ”所 在面上的数字是( )
,则图中“· ”所 在面上的数字是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com