
【题目】如图,每个立方体的![]() 个面上分别写有
个面上分别写有![]() 到
到![]() 这
这![]() 个自然数,并且任意两个相对面上所写两个数字之和为
个自然数,并且任意两个相对面上所写两个数字之和为![]() ,把这样的
,把这样的![]() 个立方体一个挨着一个地连接起来,紧挨着两个面上的数字之和为
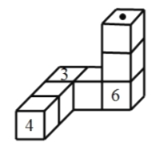
个立方体一个挨着一个地连接起来,紧挨着两个面上的数字之和为![]() ,则图中“· ”所 在面上的数字是( )
,则图中“· ”所 在面上的数字是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
【答案】B
【解析】
本题可结合题意,对图象分情况进行分析讨论即可求出结果.
由题意可知:正方体的六个面上分别写着1、2、3、4、5、6六个数,并且它们任意两个相对的面上所写的两个数的和都等于7,故第一个正方体的后面为3,
∵紧挨着的两个面上的两个数之和都等于8,则与它相接的第二个正方体的前面为5,对面为2,依此类推,与它相接的第三个正方体的前面为6,对面为1,
∴第三个正方体的左面为5,右面为2;或左面为2,右面为5.
(1)当第三个正方体的左面为5,右面为2时,第四个正方体的左面为6,右面为1,第五个正方体的左面为7(不合题意舍去);
(2)当第三个正方体的左面为2,右面为5时,第四个正方体的左面为3,右面为4,第五个正方体的左面为4,右面为3.
∴第五个正方体的下面为5,上面为2;或下面为2,上面为5.
①当第五个正方体的下面为5,上面为2时,第六个正方体的下面为6,上面为1,第七个正方体的下面为7(不合题意舍去);
②当第五个正方体的下面为2,上面为5时,第六个正方体的下面为3,上面为4,第七个正方体的下面为4,上面为3.
则“·”所在面上的数是3.
故答案为:B.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
【题目】如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是45°,向前走6m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°.
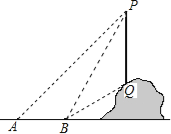
(1)求∠BPQ的度数;
(2)求该电线杆PQ的高度(结果精确到1m).
备用数据:![]() ,
,![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AM∥BN,∠A=60°,点P是射线AM上一动点(不与点A重合).BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
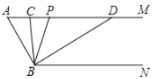
(发现)
(1)∵AM∥BN,∴∠ACB=_______;(填相等的角)
(2)求∠ABN、∠CBD的度数;
解:∵AM∥BN,
∴∠ABN+∠A=180°,
∵∠A=60°,
∴∠ABN=∠ABP+∠PBN=______,
∵BC平分∠ABP,BD平分∠PBN,
∴∠ABP=2∠CBP,∠PBN=______,
∴2∠CBP+2∠DBP=120°,
∴∠CBD=∠CBP+∠DBP=______.
(操作)
(3)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋中装有20个只有颜色不同的球,其中5个黄球,8个黑球,7个红球.
(1)求从袋中摸出一个球是黄球的概率;
(2)现从袋中取出若干个黑球,搅匀后,使从袋中摸出一个黑球的概率是![]() ,求从袋中取出黑球的个数.
,求从袋中取出黑球的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E.
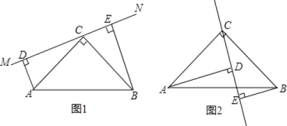
(1)求证:①△ADC≌△CEB;②DE=AD+BE.
(2)当直线MN绕点C旋转到图2的位置时,DE、AD、BE又怎样的关系?并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DEB中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是

A.BC=EC,∠B=∠E B.BC=EC,AC=DC
C.BC=DC,∠A=∠D D.∠B=∠E,∠A=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
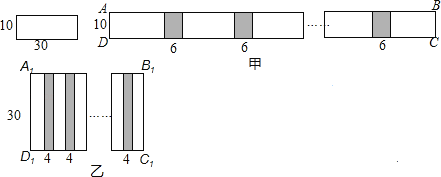
【题目】小明和小慧两位同学在数学活动课中,把长为30cm,宽为10cm的长方形白纸条粘合起来,小明按如图甲所示的方法粘合起来得到长方形ABCD,粘合部分的长度为6cm,小慧按如图乙所示的方法粘合起来得到长方形A1B1C1D1,黏合部分的长度为4cm.若长为30cm,宽为10cm的长方形白纸条共有100张,则小明应分配到 张长方形白纸条,才能使小明和小慧按各自要求黏合起来的长方形面积相等(要求100张长方形白纸条全部用完).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,分别探讨下面四个图形中∠APC与∠A,∠C的关系,请你从所得的关系中任意选取一个加以说明.
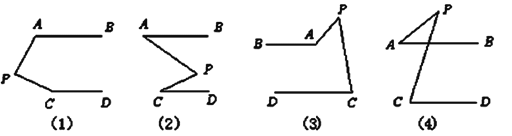
图(1)结论: ;图(2)结论: ;图(3)结论: ;图(4)结论: .
你准备证明的是图 ,请在下面写出证明过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com