
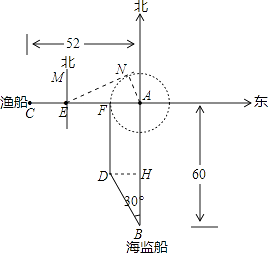
【题目】钓鱼岛历来是中国领土,以它为圆心在周围12海里范围内均属于禁区,不允许它国船只进入,如图,今有一中国海监船在位于钓鱼岛A正南方距岛60海里的B处海域巡逻,值班人员发现在钓鱼岛的正西方向52海里的C处有一艘日本渔船,正以9节的速度沿正东方向驶向钓鱼岛,中方立即向日本渔船发出警告,并沿北偏西30°的方向以12节的速度前往拦截,期间多次发出警告,2小时候海监船到达D处,与此同时日本渔船到达E处,此时海监船再次发出严重警告.
(1)当日本渔船受到严重警告信号后,必须沿北偏东转向多少度航行,才能恰好避免进入钓鱼岛12海里禁区?
(2)当日本渔船不听严重警告信号,仍按原速度,原方向继续前进,那么海监船必须尽快到达距岛12海里,且位于线段AC上的F处强制拦截渔船,问海监船能否比日本渔船先到达F处?(注:①中国海监船的最大航速为18节,1节=1海里/小时;②参考数据:sin26.3°≈0.44,sin20.5°≈0.35,sin18.1°≈0.31, ![]() ≈1.4,
≈1.4, ![]() ≈1.7)
≈1.7)
【答案】
(1)
解:过点E作圆A的切线EN,连接AN,则AN⊥EN,
由题意得,CE=9×2=18海里,则AE=AC﹣CE=52﹣18=34海里,
∵sin∠AEN= ![]() ≈0.35,
≈0.35,
∴∠AEN=20.5°,
∴∠NEM=69.5°,
即必须沿北偏东至少转向69.5°航行,才能恰好避免进入钓鱼岛12海里禁区
(2)
解:过点D作DH⊥AB于点H,
由题意得,BD=2×12=24海里,
在Rt△DBH中,DH= ![]() BD=12海里,BH=12
BD=12海里,BH=12 ![]() 海里,
海里,
∵AF=12海里,
∴DH=AF,
∴DF⊥AF,
此时海监船以最大航速行驶,
海监船到达点F的时间为: ![]() =
= ![]() =
= ![]() ≈2.2小时;
≈2.2小时;
渔船到达点F的时间为: ![]() =
= ![]() ≈2.4小时,
≈2.4小时,
∵2.2<2.4,
∴海监船比日本渔船先到达F处.
【解析】(1)过点E作圆A的切线EN,求出∠AEN的度数即可得出答案;(2)分别求出渔船、海监船到达点F的时间,然后比较可作出判断.
【考点精析】解答此题的关键在于理解关于方向角问题的相关知识,掌握指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知∠ADB=∠ADC,则不一定能使△ABD≌△ACD的条件是( )

A. AB=AC B. BD=CD C. ∠B=∠C D. ∠BAD=∠CAD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y= ![]() (x+2)(x﹣4)(k为常数,且k>0)与x轴从左至右依次交于A,B两点,与y轴交于点C,经过点B的直线y=﹣
(x+2)(x﹣4)(k为常数,且k>0)与x轴从左至右依次交于A,B两点,与y轴交于点C,经过点B的直线y=﹣ ![]() x+b与抛物线的另一交点为D.
x+b与抛物线的另一交点为D.
(1)若点D的横坐标为﹣5,求抛物线的函数表达式;
(2)若在第一象限内的抛物线上有点P,使得以A,B,P为顶点的三角形与△ABC相似,求k的值;
(3)在(1)的条件下,设F为线段BD上一点(不含端点),连接AF,一动点M从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FD以每秒2个单位的速度运动到D后停止,当点F的坐标是多少时,点M在整个运动过程中用时最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B,C的坐标分别为(1,0),(0,1),(-1,0).一个电动玩具从坐标原点O出发,第一次跳跃到点P1,使得点P1与点O关于点A成中心对称;第二次跳跃到点P2,使得点P2与点P1关于点B成中心对称;第三次跳跃到点P3,使得点P3与点P2关于点C成中心对称;第四次跳跃到点P4,使得点P4与点P3关于点A成中心对称;第五次跳跃到点P5,使得点P5与点P4关于点B成中心对称;…照此规律重复下去,则点P2105的坐标为_______________.
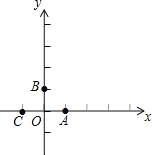
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,P是直线l外一点,点A、B、C在l上,且PB⊥l,下列说法:①PA、PB、PC这3条线段中,PB最短;②点P到直线l的距离是线段PB的长;③线段AB的长是点A到PB的距离;④线段PA的长 是点P到直线l的距离.其中正确的是( )

A.①②③
B.①②④
C.①③④
D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足 ![]() =
= ![]() ,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论: ①△ADF∽△AED;②FG=2;③tan∠E=
,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论: ①△ADF∽△AED;②FG=2;③tan∠E= ![]() ;④S△DEF=4
;④S△DEF=4 ![]() .
.
其中正确的是(写出所有正确结论的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图数轴上两点A、B所对应的数分别为-3、1,点P在数轴上从点A出发以每秒钟2个单位长度的速度向右运动,点Q在数轴上从点B出发以每秒钟1个单位长度的速度向左运动,设点P的运动时间为t秒.
(1)若点P和点Q同时出发,求点P和点Q相遇时的位置所对应的数;
(2)若点P比点Q迟1秒钟出发,问点P出发几秒后,点P和点Q刚好相距1个单位长度;
(3)在(2)的条件下,当点P和点Q刚好相距1个单位长度时,数轴上是否存在一个点C,使其到点A、点P和点Q这三点的距离和最小,若存在,直接写出点C所对应的数,若不存在,试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,把△ABC 纸片沿 DE 折叠,使点 A 落在四边形 BCED 的内部点 A′的位置,试说明 2∠A=∠1+∠2;
(2)如图②,若把△ABC 纸片沿 DE 折叠,使点 A 落在四边形 BCED 的外部点A′的位置,写出∠A 与∠1、∠2 之间的等量关系(无需说明理由);
(3)如图③,若把四边形 ABCD 沿 EF 折叠,使点 A、D 落在四边形BCFE 的内部点 A′、D′的位置,请你探索此时∠A、∠D、∠1 与∠2 之间的数量关系,写出你发现的结论并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com