
【题目】为了了解同学们对垃圾分类知识的了解程度,增强同学们的环保意识,某校数学兴趣小组设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取若干名同学进行了问卷测试.根据测试成绩分布情况,将测试成绩分成A、B、C、D四组,绘制了如下统计图表:
![]()
组别 | 分数/分 |
A | 60<x≤70 |
B | 70<x≤80 |
C | 80<x≤90 |
D | 90<x≤100 |
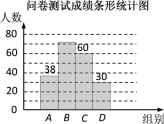
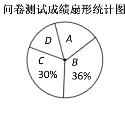
请结合以上信息解答下列问题:
(1)本次抽样调查的样本总量是多少?
(2)样本中,测试成绩在B组的频数是多少,在D组的频率是多少?
(3)样本中,这次测试成绩的中位数落在哪一组?
(4)如果该校共有800名学生,请估计成绩在90<x≤100的学生约有多少人?
【答案】(1)200;(2)72,0.15;(3)B;(4)132.
【解析】
(1)利用样本总量的定义进行求解即可;
(2)利用(1)中求出的样本总量再利用样本容量-A-C-D即可求解;利用D的频数÷样本总量即可求解;
(3)利用中位数的定义进行求解即可;
(4)先求出样本容量中D所占的百分比,然后再进行求解即可.
(1)由题意得
60÷30%=200(人),
故答案为200;
(2)B组的频数为200-38-60-30=72(人),
在D组的频率是![]() .
.
故答案为72,0.15;
(3)A组的频率为38÷200=19%,
36%+19%=55%>50%,
∴样本中,这次测试成绩的中位数落在B组.
故答案为B;
(4)![]() (人).
(人).
故答案为132.


科目:初中数学 来源: 题型:
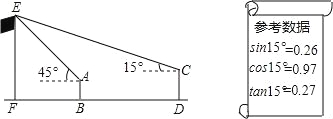
【题目】某校九(18)班开展数学活动,毓齐和博文两位同学合作用测角仪测量学校的旗杆,毓齐站在B点测得旗杆顶端E点的仰角为45°,博文站在D(D点在直线FB上)测得旗杆顶端E点仰角为15°,已知毓齐和博文相距(BD)30米,毓齐的身高(AB)1.6米,博文的身高(CD)1.75米,求旗杆的高EF的长.(结果精确到0.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一条河的两岸BC与DE互相平行,两岸各有一排景观灯(图中黑点代表景观灯),每排相邻两景观灯的间隔都是10 m,在与河岸DE的距离为16 m的A处(AD⊥DE)看对岸BC,看到对岸BC上的两个景观灯的灯杆恰好被河岸DE上两个景观灯的灯杆遮住.河岸DE上的两个景观灯之间有1个景观灯,河岸BC上被遮住的两个景观灯之间有4个景观灯,求这条河的宽度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB和抛物线的交点是A(0,-3),B(5,9),已知抛物线的顶点D的横坐标是2.

(1)求抛物线的解析式及顶点坐标;
(2)在![]() 轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)在直线AB的下方抛物线上找一点P,连接PA,PB使得△PAB的面积最大,并求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,某超市从一楼到二楼有一自动扶梯,图2是侧面示意图.已知自动扶梯AB的坡度为1:2.4,AB的长度是13米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角为42°,求二楼的层高BC约为多少米?( sin42°≈0.7,tan42°≈0.9)

查看答案和解析>>
科目:初中数学 来源: 题型:
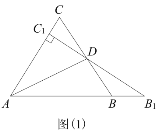
【题目】如图(1)所示,等边△ABC中,线段AD为其内角角平分线,过D点的直线B1C1⊥AC于点C1交AB的延长线于点B1.
(1)请你探究:![]() =
=![]() ,
,![]() =
=![]() 是否都成立?
是否都成立?
(2)请你继续探究:若△ABC为任意三角形,线段AD为其内角角平分线,请问![]() =
=![]() 一定成立吗?并证明你的判断.
一定成立吗?并证明你的判断.
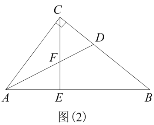
(3)如图(2)所示Rt△ABC中,∠ACB=90°,AC=8,AB=![]() ,E为AB上一点且AE=5,CE交其内角角平分线AD于F.试求
,E为AB上一点且AE=5,CE交其内角角平分线AD于F.试求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
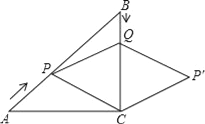
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC=6cm,点P从点A出发,沿AB方向以每秒![]() cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′,设Q点运动的时间为t秒,若四边形QPCP′为菱形,则t的值为_____.
cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′,设Q点运动的时间为t秒,若四边形QPCP′为菱形,则t的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,动点P从直角梯形ABCD的直角顶点B出发,沿BCDA的顺序运动,得到以点P移动的路程x为自变量,△ABP面积y为函数的图象,如图2,则梯形ABCD的面积是( )
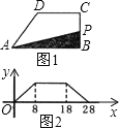
A. 104B. 120C. 80D. 112
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com