
����Ŀ�����ֽ�����+����ʱ�������������ǵ������Ѿ������������ܲ��ɷ�.�����硰![]() �������յȼ����������ױ��ƽ⣬������ü�������һ�������������ͺ��б�Ҫ��.��һ���á���ʽ�ֽ⡱�����������룬������䣬��ԭ���ǣ���һ������ʽ�ֽ���ʽ���罫����ʽ
�������յȼ����������ױ��ƽ⣬������ü�������һ�������������ͺ��б�Ҫ��.��һ���á���ʽ�ֽ⡱�����������룬������䣬��ԭ���ǣ���һ������ʽ�ֽ���ʽ���罫����ʽ![]() ��ʽ�ֽ�Ľ��Ϊ
��ʽ�ֽ�Ľ��Ϊ![]() ����
����![]() ʱ��
ʱ��![]() ��
��![]() ��
��![]() ����ʱ���Եõ���������
����ʱ���Եõ���������![]() ��
��![]() ��.
��.
��1������������������![]() ��
��![]() ʱ�����ڶ���ʽ
ʱ�����ڶ���ʽ![]() �ֽ���ʽ������γ���Щ�������루д���ĸ����ɣ�?
�ֽ���ʽ������γ���Щ�������루д���ĸ����ɣ�?
��2��������ʽ![]() ��ʽ�ֽ������һ��ʽ�ij˻���������Ŀ����ʾ�ķ�������
��ʽ�ֽ������һ��ʽ�ij˻���������Ŀ����ʾ�ķ�������![]() ʱ���Եõ�����
ʱ���Եõ�����![]() ����
����![]() ��
��![]() ��ֵ.
��ֵ.

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC����BAC=90������D�DZ�BC�ϵĶ��㣬����AD����C����ֱ��AD�ĶԳƵ�Ϊ��E������BE������AD���ڵ�F.


��1����ͼ1�У������ⲹȫͼ�Σ�
��2����![]() ��
��![]() ������
������![]() �Ĵ�С�����ú�
�Ĵ�С�����ú�![]() ��ʽ�ӱ�ʾ��
��ʽ�ӱ�ʾ��
��3������ACE�ǵȱ������Σ�����EF��BC��������ϵ����֤��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O��CE��BD��DE��AC����AC=4�����ı���OCED���ܳ�Ϊ��������

A. 4 B. 8 C. 10 D. 12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() �ǵȱ������Σ�
�ǵȱ������Σ�![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() ���е㣬��
���е㣬��![]() .
.![]() ��
��![]() ��һ���㣬��
��һ���㣬��![]() ����СֵΪ___________
����СֵΪ___________![]() .
.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڳ�����![]() �У�
��![]() ��
��![]() ����
����![]() �ӵ�
�ӵ�![]() ��������
��������![]() ���ٶ���
���ٶ���![]() ���
���![]() �˶������
�˶������![]() ���˶�ʱ��Ϊ
���˶�ʱ��Ϊ![]() �룬��
�룬��![]() .
.

��1��![]() _________
_________![]() ���ú�
���ú�![]() �Ĵ���ʽ��ʾ��.
�Ĵ���ʽ��ʾ��.
��2����ͼ������![]() �ӵ�
�ӵ�![]() ��ʼ�˶���ͬʱ����
��ʼ�˶���ͬʱ����![]() �ӵ�
�ӵ�![]() ��������
��������![]() ���ٶ���
���ٶ���![]() ���
���![]() �˶����Ƿ����������
�˶����Ƿ����������![]() ֵ��ʹ����
ֵ��ʹ����![]() ��
��![]() ��
��![]() ���������������
���������������![]() ��
��![]() ��
��![]() Ϊ�����������ȫ��?�����ڣ������v��ֵ���������ڣ���˵������.
Ϊ�����������ȫ��?�����ڣ������v��ֵ���������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
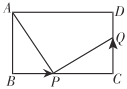
����Ŀ����ͼ��ֱ������ABCD�У���C=��D=90����AD��BC��BC=CD=6��E�DZ�CD�ϵ�һ�㣬ǡ��ʹAE=5�����ҡ�ABE=45�㣬��CE�ij���___________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ����������ϵ![]() �У�ֱ��
�У�ֱ��![]() ��
��![]() �ᣬ
�ᣬ![]() ��ֱ��ڵ�
��ֱ��ڵ�![]() ����
����![]() ����
����![]() ��
��![]() ��ĸ������ϣ�����
��ĸ������ϣ�����![]() ��ֱ��
��ֱ��![]() �۵�����
�۵�����![]() ǡ������
ǡ������![]() ���������ϵĵ�
���������ϵĵ�![]() ��.
��.

��1��ֱ��д��![]() �ij�_________��
�ij�_________��
��2����ֱ��![]() �ĺ�������ʽ��
�ĺ�������ʽ��
��3�����![]() �͵�
�͵�![]() �����ꣻ
�����ꣻ
��4��![]() �����Ƿ����һ��
�����Ƿ����һ��![]() ��ʹ��
��ʹ��![]() �������ڣ�ֱ��д����
�������ڣ�ֱ��д����![]() �����ꣻ�������ڣ���˵������.
�����ꣻ�������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڰ�˫�ۣ��ݺὭ����˫����赣������У���������С˵�еij�������������˼��ָ�����˺���һ��ȡ�����̣������ޱȣ��ڶ��θ�ʽ��Ҳ���������ศ��ɵ������������磺![]() �����ǵĻ��в������ţ�����˵���������θ�ʽ��Ϊ��������ʽ������һ������һ������������ʽ�����ǣ����θ�ʽ�������������⣺
�����ǵĻ��в������ţ�����˵���������θ�ʽ��Ϊ��������ʽ������һ������һ������������ʽ�����ǣ����θ�ʽ�������������⣺
 .
.
������ͨ�����ӡ���ĸͬ��һ��ʽ�Ӱѷ�ĸ�еĸ��Ż�ȥ�ķ�����������ĸ��������
������⣺
��1��![]() ����������ʽ�� ��
����������ʽ�� ��
��![]() ��ĸ�������� ��
��ĸ�������� ��
��2����֪��![]() ����
����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ�����ͼ����x�ύ��A����3��0����B��1��0�����㣬��y���ڵ�C��0��3������C��D�Ƕ��κ���ͼ���ϵ�һ�ԶԳƵ㣬һ�κ�����ͼ�����B��D��
��1����ֱ��д��D������꣮
��2������κ����Ľ���ʽ��
��3������ͼ��ֱ��д��ʹһ�κ���ֵ���ڶ��κ���ֵ��x��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com