
【题目】定义:若函数![]() 与
与![]() 轴的交点
轴的交点![]() 的横坐标为
的横坐标为![]() ,
,![]() ,与
,与![]() 轴交点的纵坐标为
轴交点的纵坐标为![]() ,若
,若![]() ,
,![]() 中至少存在一个值,满足
中至少存在一个值,满足![]() (或
(或![]() ),则称该函数为友好函数.如图,函数
),则称该函数为友好函数.如图,函数![]() 与
与![]() 轴的一个交点
轴的一个交点![]() 的横坐标为-3,与
的横坐标为-3,与![]() 轴交点
轴交点![]() 的纵坐标为-3,满足
的纵坐标为-3,满足![]() ,称
,称![]() 为友好函数.
为友好函数.
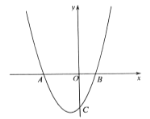
(1)判断![]() 是否为友好函数,并说明理由;
是否为友好函数,并说明理由;
(2)请探究友好函数![]() 表达式中的
表达式中的![]() 与
与![]() 之间的关系;
之间的关系;
(3)若![]() 是友好函数,且
是友好函数,且![]() 为锐角,求
为锐角,求![]() 的取值范围.
的取值范围.
【答案】(1)是,理由见解析;(2)![]() ;(3)
;(3)![]() 或
或![]() ,且
,且![]()
【解析】
(1)根据友好函数的定义,求出函数与x轴交点的横坐标以及与y轴交点的纵坐标,即可进行判断;
(2)先求出函数与y轴交点的纵坐标为c,再根据定义,可得当x=c时,y=0,据此可得出结果;
(3)分一下三种情况求解:(ⅰ)当![]() 在
在![]() 轴负半轴上时,由(2)可得:
轴负半轴上时,由(2)可得:![]() ,进而可得出结果;(ⅱ)当
,进而可得出结果;(ⅱ)当![]() 在
在![]() 轴正半轴上时,且
轴正半轴上时,且![]() 与
与![]() 不重合时,画出图像可得出结果;(ⅲ)当
不重合时,画出图像可得出结果;(ⅲ)当![]() 与原点重合时,不符合题意.
与原点重合时,不符合题意.
解:(1)![]() 是友好函数.理由如下:
是友好函数.理由如下:
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() 或3,
或3,
∴![]() 与
与![]() 轴一个交点的横坐标和与
轴一个交点的横坐标和与![]() 轴交点的纵坐标都是3.
轴交点的纵坐标都是3.
故![]() 是友好函数.
是友好函数.
(2)当![]() 时,
时,![]() ,即与
,即与![]() 轴交点的纵坐标为
轴交点的纵坐标为![]() .
.
∵![]() 是友好函数.
是友好函数.
∴![]() 时,
时,![]() ,即
,即![]() 在
在![]() 上.
上.
代入得:![]() ,而
,而![]() ,∴
,∴![]() .
.
(3)(ⅰ)当![]() 在
在![]() 轴负半轴上时,由(2)可得:
轴负半轴上时,由(2)可得:![]() ,
,
即![]() ,显然当
,显然当![]() 时,
时,![]() ,
,
即与![]() 轴的一个交点为
轴的一个交点为![]() .
.
则![]() ,∴只需满足
,∴只需满足![]() ,即
,即![]() .
.
∴![]() .
.
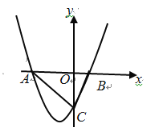
(ⅱ)当![]() 在
在![]() 轴正半轴上时,且
轴正半轴上时,且![]() 与
与![]() 不重合时,
不重合时,
∴显然都满足![]() 为锐角.
为锐角.
∴![]() ,且
,且![]() .
.
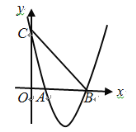
(ⅲ)当![]() 与原点重合时,不符合题意.
与原点重合时,不符合题意.
综上所述,![]() 或
或![]() ,且
,且![]() .
.


科目:初中数学 来源: 题型:
【题目】综合与实践:
操作与发现:
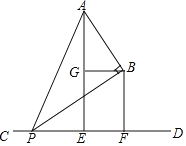
如图,已知A,B两点在直线CD的同一侧,线段AE,BF均是直线CD的垂线段,且BF在AE的右边,AE=2BF,将BF沿直线CD向右平移,在平移过程中,始终保持∠ABP=90°不变,BP边与直线CD相交于点P,点G是AE的中点,连接BG.
探索与证明:求证:
(1)四边形EFBG是矩形;
(2)△ABG∽△PBF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师布置了一个作业,如下:已知:如图1![]() 的对角线
的对角线![]() 的垂直平分线
的垂直平分线![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .求证:四边形
.求证:四边形![]() 是菱形.
是菱形.
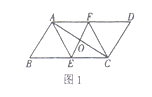

某同学写出了如图2所示的证明过程,老师说该同学的作业是错误的.请你解答下列问题:
(1)能找出该同学错误的原因吗?请你指出来;
(2)请你给出本题的正确证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】空间任意选定一点![]() ,以点
,以点![]() 为端点作三条互相垂直的射线
为端点作三条互相垂直的射线![]() ,
,![]() ,
,![]() .这三条互相垂直的射线分别称作
.这三条互相垂直的射线分别称作![]() 轴、
轴、![]() 轴、
轴、![]() 轴,统称为坐标轴,它们的方向分别为
轴,统称为坐标轴,它们的方向分别为![]() (水平向前),
(水平向前),![]() (水平向右),
(水平向右),![]() (竖直向上)方向,这样的坐标系称为空间直角坐标系.将相邻三个面的面积记为
(竖直向上)方向,这样的坐标系称为空间直角坐标系.将相邻三个面的面积记为![]() ,且
,且![]() 的小长方体称为单位长方体,现将若干个单位长方体在空间直角坐标系内进行码放,要求码放时将单位长方体
的小长方体称为单位长方体,现将若干个单位长方体在空间直角坐标系内进行码放,要求码放时将单位长方体![]() 所在的面与
所在的面与![]() 轴垂直,
轴垂直,![]() 所在的面与
所在的面与![]() 轴垂直,
轴垂直,![]() 所在的面与
所在的面与![]() 轴垂直,如图
轴垂直,如图![]() 所示.若将
所示.若将![]() 轴方向表示的量称为几何体码放的排数,
轴方向表示的量称为几何体码放的排数,![]() 轴方向表示的量称为几何体码放的列数,
轴方向表示的量称为几何体码放的列数,![]() 轴方向表示的量称为几何体码放的层数;如图
轴方向表示的量称为几何体码放的层数;如图![]() 是由若干个单位长方体在空间直角坐标内码放的一个几何体,其中这个几何体共码放了
是由若干个单位长方体在空间直角坐标内码放的一个几何体,其中这个几何体共码放了![]() 排
排![]() 列
列![]() 层,用有序数组记作 (1,2,6),如图
层,用有序数组记作 (1,2,6),如图![]() 的几何体码放了
的几何体码放了![]() 排
排![]() 列
列![]() 层,用有序数组记作 (2,3,4).这样我们就可用每一个有序数组
层,用有序数组记作 (2,3,4).这样我们就可用每一个有序数组![]() 表示一种几何体的码放方式.
表示一种几何体的码放方式.
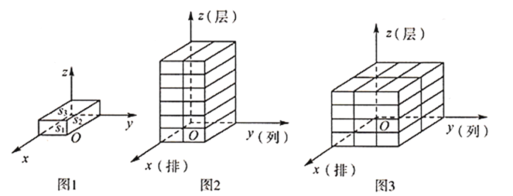
(1)有序数组 (3,2,4)所对应的码放的几何体是_____;

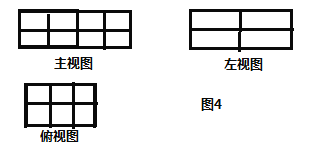
(2)图![]() 是由若干个单位长方体码放的一个几何体的三视图,则这种码放方式的有序数组为(___,____,____),组成这个几何体的单位长方体的个数为____个;
是由若干个单位长方体码放的一个几何体的三视图,则这种码放方式的有序数组为(___,____,____),组成这个几何体的单位长方体的个数为____个;
(3)为了进一步探究有序数组![]() 的几何体的表面积公式
的几何体的表面积公式![]() ,某同学针对若干个单位长方体进行码放,制作了下列表格:
,某同学针对若干个单位长方体进行码放,制作了下列表格:
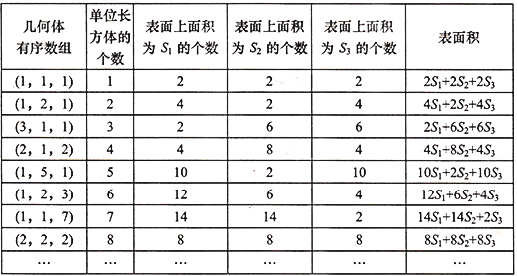
根据以上规律,请直接写出有序数组![]() 的几何体表面积
的几何体表面积![]() 的计算公式;(用
的计算公式;(用![]() 表示)
表示)
(4)当![]() 时,对由
时,对由![]() 个单位长方体码放的几何体进行打包,为了节约外包装材料,我们可以对
个单位长方体码放的几何体进行打包,为了节约外包装材料,我们可以对![]() 个单位长方体码放的几何体表面积最小的规律进行探究,请你根据自己探究的结果直接写出使几何体表面积最小的有序数组,这个有序数组为(___,___,___),此时求出的这个几何体表面积的大小为________.(缝隙不计)
个单位长方体码放的几何体表面积最小的规律进行探究,请你根据自己探究的结果直接写出使几何体表面积最小的有序数组,这个有序数组为(___,___,___),此时求出的这个几何体表面积的大小为________.(缝隙不计)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由24个小正方形组成的网格图,每一个正方形的顶点都称为格点,![]() 的三个顶点都是格点.请按要求完成下列作图,每个小题只需作出一个符合条件的图形.
的三个顶点都是格点.请按要求完成下列作图,每个小题只需作出一个符合条件的图形.
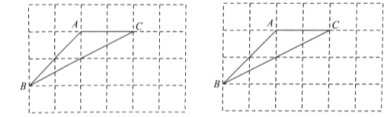
(1)在图1网格中找格点![]() ,作直线
,作直线![]() ,使直线
,使直线![]() 平分
平分![]() 的面积;
的面积;
(2)在图2网格中找格点![]() ,作直线
,作直线![]() ,使直线
,使直线![]() 把
把![]() 的面积分成
的面积分成![]() 两部分.
两部分.
查看答案和解析>>
科目:初中数学 来源: 题型:
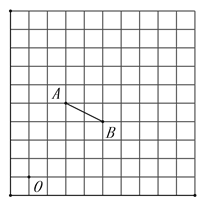
【题目】如图,在由边长为1个单位长度的小正方形组成的10×10网格中,已知点O,A,B均为网格线的交点.
(1)在给定的网格中,以点O为位似中心,将线段AB放大为原来的2倍,得到线段![]() (点A,B的对应点分别为
(点A,B的对应点分别为![]() ).画出线段
).画出线段![]() ;
;
(2)将线段![]() 绕点
绕点![]() 逆时针旋转90°得到线段
逆时针旋转90°得到线段![]() .画出线段
.画出线段![]() ;
;
(3)以![]() 为顶点的四边形
为顶点的四边形![]() 的面积是 个平方单位.
的面积是 个平方单位.
查看答案和解析>>
科目:初中数学 来源: 题型:
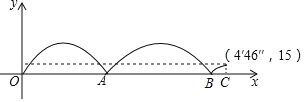
【题目】某中学举办运动会,在1500米的项目中,参赛选手在200米的环形跑道上进行,如图记录了跑的最快的一位选手与最慢的一位选手的跑步过程(最快的选手跑完了全程),其中x表示最快的选手的跑步时间,y表示这两位选手之间的距离,现有以下4种说法,正确的有( )
①最快的选手到达终点时,最慢的选手还有15米未跑;
②跑的最快的选手用时4'46″;
③出发后最快的选手与最慢的选手相遇了两次;
④出发后最快的选手与最慢的选手第一次相遇比第二次相遇的用时长.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体试验,测得成人服药后血液中药物浓度y(微克/毫升)与服药时间x小时之间函数关系如图所示(当4≤x≤10时,y与x成反比例).
(1)根据图象分别求出血液中药物浓度上升和下降阶段y与x之间的函数关系式.
(2)问血液中药物浓度不低于2微克/毫升的持续时间多少小时?

查看答案和解析>>
科目:初中数学 来源: 题型:
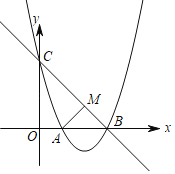
【题目】已知抛物线![]() 过点
过点![]() ,
,![]() 两点,与y轴交于点C,
两点,与y轴交于点C,![]() .
.
(1)求抛物线的解析式及顶点D的坐标;
(2)过点A作![]() ,垂足为M,求证:四边形ADBM为正方形;
,垂足为M,求证:四边形ADBM为正方形;
(3)点P为抛物线在直线BC下方图形上的一动点,当![]() 面积最大时,求点P的坐标;
面积最大时,求点P的坐标;
(4)若点Q为线段OC上的一动点,问:![]() 是否存在最小值?若存在,求岀这个最小值;若不存在,请说明理由.
是否存在最小值?若存在,求岀这个最小值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com