
【题目】已知抛物线![]() 过点
过点![]() ,
,![]() 两点,与y轴交于点C,
两点,与y轴交于点C,![]() .
.
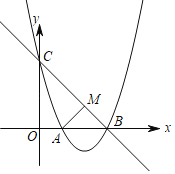
(1)求抛物线的解析式及顶点D的坐标;
(2)过点A作![]() ,垂足为M,求证:四边形ADBM为正方形;
,垂足为M,求证:四边形ADBM为正方形;
(3)点P为抛物线在直线BC下方图形上的一动点,当![]() 面积最大时,求点P的坐标;
面积最大时,求点P的坐标;
(4)若点Q为线段OC上的一动点,问:![]() 是否存在最小值?若存在,求岀这个最小值;若不存在,请说明理由.
是否存在最小值?若存在,求岀这个最小值;若不存在,请说明理由.
【答案】(1)抛物线的表达式为:![]() ,顶点
,顶点![]() ;(2)证明见解析;(3)点
;(2)证明见解析;(3)点![]() ;(4)存在,
;(4)存在,![]() 的最小值为
的最小值为![]() .
.
【解析】
(1)设交点式![]() ,利用待定系数法进行求解即可;
,利用待定系数法进行求解即可;
(2)先证明四边形ADBM为菱形,再根据有一个角是直角的菱形是正方形即可得证;
(3)先求出直线BC的解析式,过点P作y轴的平行线交BC于点N,设点![]() ,则点N
,则点N![]() ,根据
,根据![]() 可得关于x的二次函数,继而根据二次函数的性质进行求解即可;
可得关于x的二次函数,继而根据二次函数的性质进行求解即可;
(4)存在,如图,过点C作与y轴夹角为![]() 的直线CF交x轴于点F,过点A作
的直线CF交x轴于点F,过点A作![]() ,垂足为H,交y轴于点Q, 此时
,垂足为H,交y轴于点Q, 此时![]() ,则
,则![]() 最小值
最小值![]() ,求出直线HC、AH的解析式即可求得H点坐标,进行求得AH的长即可得答案.
,求出直线HC、AH的解析式即可求得H点坐标,进行求得AH的长即可得答案.
(1)函数的表达式为:![]() ,
,
即:![]() ,解得:
,解得:![]() ,
,
故抛物线的表达式为:![]() ,
,
则顶点![]() ;
;
(2)![]() ,
,![]() ,
,
∵A(1,0),B(3,0),∴ OB=3,OA=1,
∴AB=2,
∴![]() ,
,
又∵D(2,-1),
∴AD=BD=![]() ,
,
∴AM=MB=AD=BD,
∴四边形ADBM为菱形,
又∵![]() ,
,
![]() 菱形ADBM为正方形;
菱形ADBM为正方形;
(3)设直线BC的解析式为y=mx+n,
将点B、C的坐标代入得:![]() ,
,
解得:![]() ,
,
所以直线BC的表达式为:y=-x+3,
过点P作y轴的平行线交BC于点N,
设点![]() ,则点N
,则点N![]() ,
,
则![]() ,
,
![]() ,故
,故![]() 有最大值,此时
有最大值,此时![]() ,
,
故点![]() ;
;
(4)存在,理由:
如图,过点C作与y轴夹角为![]() 的直线CF交x轴于点F,过点A作
的直线CF交x轴于点F,过点A作![]() ,垂足为H,交y轴于点Q,
,垂足为H,交y轴于点Q,
此时![]() ,
,
则![]() 最小值
最小值![]() ,
,
在Rt△COF中,∠COF=90°,∠FOC=30°,OC=3,tan∠FCO=![]() ,
,
∴OF=![]() ,
,
∴F(-![]() ,0),
,0),
利用待定系数法可求得直线HC的表达式为:![]() …①,
…①,
∵∠COF=90°,∠FOC=30°,
∴∠CFO=90°-30°=60°,
∵∠AHF=90°,
∴∠FAH=90°-60°=30°,
∴OQ=AOtan∠FAQ=![]() ,
,
∴Q(0,![]() ),
),
利用待定系数法可求得直线AH的表达式为:![]() …②,
…②,
联立①②并解得:![]() ,
,
故点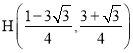 ,而点
,而点![]() ,
,
则![]() ,
,
即![]() 的最小值为
的最小值为![]() .
.


科目:初中数学 来源: 题型:
【题目】定义:若函数![]() 与
与![]() 轴的交点
轴的交点![]() 的横坐标为
的横坐标为![]() ,
,![]() ,与
,与![]() 轴交点的纵坐标为
轴交点的纵坐标为![]() ,若
,若![]() ,
,![]() 中至少存在一个值,满足
中至少存在一个值,满足![]() (或
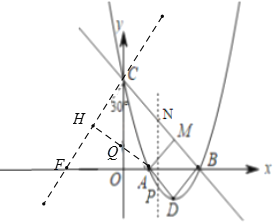
(或![]() ),则称该函数为友好函数.如图,函数
),则称该函数为友好函数.如图,函数![]() 与
与![]() 轴的一个交点
轴的一个交点![]() 的横坐标为-3,与
的横坐标为-3,与![]() 轴交点
轴交点![]() 的纵坐标为-3,满足
的纵坐标为-3,满足![]() ,称
,称![]() 为友好函数.
为友好函数.
(1)判断![]() 是否为友好函数,并说明理由;
是否为友好函数,并说明理由;
(2)请探究友好函数![]() 表达式中的
表达式中的![]() 与
与![]() 之间的关系;
之间的关系;
(3)若![]() 是友好函数,且
是友好函数,且![]() 为锐角,求
为锐角,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
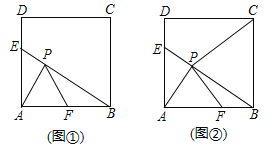
【题目】如图,边长为6的正方形![]() 中,
中,![]() 分别是
分别是![]() 上的点,
上的点,![]() ,
,![]() 为垂足.
为垂足.
(1)如图①, AF=BF,AE=2![]() ,点T是射线PF上的一个动点,则当△ABT为直角三角形时,求AT的长;
,点T是射线PF上的一个动点,则当△ABT为直角三角形时,求AT的长;
(2)如图②,若![]() ,连接
,连接![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校艺术节计划为学生购买A、B两种奖品,已知购买40件A种奖品和购买60件B种奖品共需2600元,购买35件A种奖品和购买70件B种奖品共需2800元.
(1)求A、B两种奖品的单价各为多少元?
(2)若学校购买A、B两种奖品共100件,且购买这批奖品的总费用不超过2800元,求最多购买B奖品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
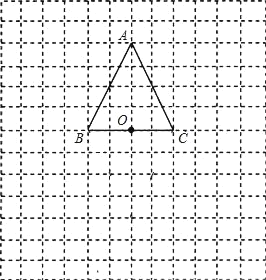
【题目】在如图所示的方格纸中,将等腰△ABC绕底边BC的中点O旋转180°.
(1)画出旋转后的图形;
(2)观察:旋转后得到的三角形与原三角形拼成什么图形?
(3)若要使拼成的图形为正方形,那么△ABC应满足什么条件?
查看答案和解析>>
科目:初中数学 来源: 题型:
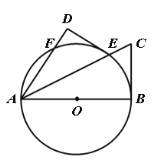
【题目】如图,已知AB是⊙O的直径,F是⊙O上一点,∠BAF的平分线交⊙O于点E,交⊙O的切线BC于点C,过点E作ED⊥AF,交AF的延长线于点D.
(1)求证:DE是⊙O的切线;
(2)若DE=3,CE=2,
①求![]() 值;
值;
②若点G 为AE上一点,求OG+![]() EG最小值.
EG最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上运动,连接
上运动,连接![]() ,以
,以![]() 为一边且在
为一边且在![]() 的右侧作正方形
的右侧作正方形![]() .
.
(1)如果![]() ,如图①,试判断线段
,如图①,试判断线段![]() 与
与![]() 之间的位置关系,并证明你的结论;
之间的位置关系,并证明你的结论;
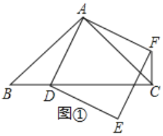
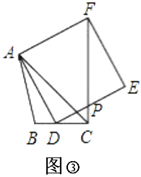
(2)如果![]() ,如图②,(1)中结论是否成立,说明理由.
,如图②,(1)中结论是否成立,说明理由.
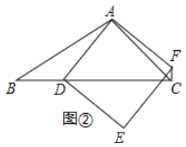
(3)如果![]() ,如图③,且正方形
,如图③,且正方形![]() 的边
的边![]() 与线段
与线段![]() 交于点
交于点![]() ,设
,设![]() ,
,![]() ,
,![]() ,请直接写出线段
,请直接写出线段![]() 的长.(用含
的长.(用含![]() 的式子表示)
的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】庐阳春风体育运动品商店从厂家购进甲,乙两种T恤共400件,其每件的售价与进货量![]() (件)之间的关系及成本如下表所示:
(件)之间的关系及成本如下表所示:
T恤 | 每件的售价/元 | 每件的成本/元 |
甲 |
| 50 |
乙 |
| 60 |
|
(1)当甲种T恤进货250件时,求两种T恤全部售完的利润是多少元;
(2)若所有的T恤都能售完,求该商店获得的总利润![]() (元)与乙种T恤的进货量
(元)与乙种T恤的进货量![]() (件)之间的函数关系式;
(件)之间的函数关系式;
(3)在(2)的条件下,已知两种T恤进货量都不低于100件,且所进的T恤全部售完,该商店如何安排进货才能使获得的利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,已知
,已知![]() ,
,![]() .
.

(1)求抛物线的解析式;
(2)如图2,若点![]() 是直线
是直线![]() 上方的抛物线上一动点,过点
上方的抛物线上一动点,过点![]() 作
作![]() 轴的平行线交直线
轴的平行线交直线![]() 于点
于点![]() ,作
,作![]() 于点
于点![]() ,当点
,当点![]() 的横坐标为
的横坐标为![]() 时,求
时,求![]() 的面积;
的面积;
(3)若点![]() 为抛物线上的一个动点,以点
为抛物线上的一个动点,以点![]() 为圆心,
为圆心,![]() 为半径作
为半径作![]() ,当
,当![]() 在运动过程中与直线
在运动过程中与直线![]() 相切时,求点
相切时,求点![]() 的坐标(请直接写出答案).
的坐标(请直接写出答案).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com