
【题目】如图,边长为6的正方形![]() 中,
中,![]() 分别是
分别是![]() 上的点,
上的点,![]() ,
,![]() 为垂足.
为垂足.
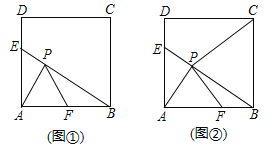
(1)如图①, AF=BF,AE=2![]() ,点T是射线PF上的一个动点,则当△ABT为直角三角形时,求AT的长;
,点T是射线PF上的一个动点,则当△ABT为直角三角形时,求AT的长;
(2)如图②,若![]() ,连接
,连接![]() ,求证:
,求证:![]() .
.
【答案】(1) 3或3![]() 或3
或3![]() ;(2)见解析.
;(2)见解析.
【解析】分析:(1)解Rt△BAE,由tan∠ABE=![]() =
=![]() ,得出∠ABE=30°.然后分三种情况进行讨论:①当点T在AB的上方,∠ATB=90°时,显然点T和点P重合,易求AT=AP=
,得出∠ABE=30°.然后分三种情况进行讨论:①当点T在AB的上方,∠ATB=90°时,显然点T和点P重合,易求AT=AP=![]() AB=3;②当点T在AB的下方,∠ATB=90°时,根据直角三角形斜边上的中线等于斜边的一半可得TF=BF=AF=3,而∠BFT=60°,那么 △FTB是等边三角形,TB=3,再根据勾股定理求出AT=
AB=3;②当点T在AB的下方,∠ATB=90°时,根据直角三角形斜边上的中线等于斜边的一半可得TF=BF=AF=3,而∠BFT=60°,那么 △FTB是等边三角形,TB=3,再根据勾股定理求出AT=![]() =3
=3![]() ;
;
③当点T在AB的下方,∠ABT=90°时.在Rt△ATB中利用勾股定理求出AT;
(2)先证明∠1=∠3=∠4,由tan∠1=![]() ,tan∠3=
,tan∠3=![]() ,得出
,得出![]() =
=![]() ,等量代换得到
,等量代换得到![]() =
=![]() .再证明△PBC∽△PAF,得出∠5=∠6,进而可得∠5+∠7=90°,即∠CPF=90°,那么CP⊥FP.
.再证明△PBC∽△PAF,得出∠5=∠6,进而可得∠5+∠7=90°,即∠CPF=90°,那么CP⊥FP.
详解:(1)在正方形ABCD中,可得∠DAB=90°.
∵在Rt△BAE中,tan∠ABE=![]() =
=![]() =
=![]() ,∴∠ABE=30°.
,∴∠ABE=30°.
点T是射线PF上的一个动点,当△ABT为直角三角形时,分三种情况:
①当点T在AB的上方,∠ATB=90°,显然此时点T和点P重合,即AT=AP=![]() AB=3;
AB=3;
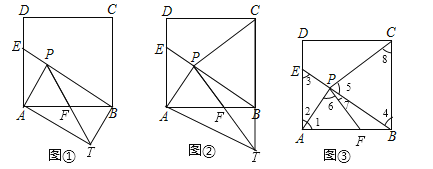
②当点T在AB的下方,∠ATB=90°,如图①所示.
在Rt△APB中,由AF=BF,可得:AF=BF=PF=3,∴∠BPF=∠FBP=30°,∴∠BFT=60°.
在Rt△ATB中,TF=BF=AF=3,∴△FTB是等边三角形,∴TB=3,AT=![]() =3
=3![]() ;
;
③当点T在AB的下方,∠ABT=90°时,如图②所示.
在Rt△FBT中,∠BFT=60°,BF=3,BT=BFtan60°=3![]() .
.
在Rt△ATB中:AT=![]() =3
=3![]() .
.
综上所述:当△ABT为直角三角形时,AT的长为3或3![]() 或3
或3![]() ;
;
(2)如图③所示.
∵四边形ABCD是正方形,∴AB=AD=BC,AD∥BC,∠DAB=90°,∴∠3=∠4.
∵在Rt△EAB中,AP⊥BE,∴∠1+∠2=90°,∠3+∠2=90°,∴∠1=∠3,∴∠1=∠3=∠4.
∵tan∠1=![]() ,tan∠3=
,tan∠3=![]() =
=![]() .
.
∵AE=AF,AB=BC,∴![]() =
=![]() .
.
在△PBC和△PAF中,∵![]() ,∠4=∠1,∴△PBC∽△PAF,∴∠5=∠6.
,∠4=∠1,∴△PBC∽△PAF,∴∠5=∠6.
∵∠6+∠7=90/span>°,∴∠5+∠7=90°,即∠CPF=90°,∴CP⊥FP.


科目:初中数学 来源: 题型:
【题目】![]() 、
、![]() 两地相距
两地相距![]() ,甲、乙两车分别沿同一条路线从
,甲、乙两车分别沿同一条路线从![]() 地出发驶往
地出发驶往![]() 地,已知甲车的速度为
地,已知甲车的速度为![]() ,乙车的速度为
,乙车的速度为![]() ,甲车先出发
,甲车先出发![]() 后乙车再出发,乙车到达
后乙车再出发,乙车到达![]() 地后再原地等甲车.
地后再原地等甲车.
(1)求乙车出发多长时间追上甲车?
(2)求乙车出发多长时间与甲车相距![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )

A.  B.
B. 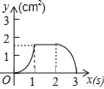 C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车在公路上行驶,看到里程表上是一个两位数,1小时后其里程表还是一个两位数,且刚好它的十位数字与个位数字与第一次看到的两位数的十位数字与个位数字颠倒了位置,又过了1小时后看到里程表是一个三位数,它是第一次看到的两位数中间加一个0,则汽车的速度是( )千米/小时.
A. 35B. 40C. 45D. 50
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明从家去体育场锻炼,同时,妈妈从体育场以50米/分的速度回家,小明到体育场后发现要下雨,立即返回,追上妈妈后,小明以250米/分的速度回家取伞,立即又以250米/分的速度折回接妈妈,并一同回家.如图是两人离家的距离y(米)与小明出发的时间x(分)之间的函数图像.
(注:小明和妈妈始终在同一条笔直的公路上行走,图像上A、C、D三点在一条直线上)
(1)求线段BC的函数表达式;
(2)求点D坐标;
(3)当 x的值为 时,小明与妈妈相距1 500米.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com