
【题目】如图,直线AB、CD相交于点O,OE⊥CD,OF平分∠BOD.
(1)图中除直角外,请写出一对相等的角吗: (写出符合的一对即可)
(2)如果∠AOE=26°,求∠BOD和∠COF的度数.(所求的角均小于平角)
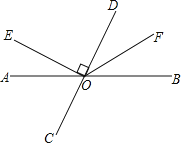
【答案】(1)∠DOF=∠BOF;(2)∠BOD=64°,∠COF=148°.
【解析】试题分析:(1)利用角平分线的性质可得∠DOF=∠BOF;(2)已知OE⊥CD,根据垂直的定义可得∠COE=90°,根据∠AOC=∠COE﹣∠AOE求得∠AOC的度数,根据对顶角相等可得∠AOC=∠BOD,又因OF平分∠BOD,可求得∠DOF的度数,再由∠COF=180°﹣∠DOF即可求得∠COF的度数.
试题解析:
(1)∠DOF=∠BOF
(2)∵OE⊥CD,
∴∠COE=90°,
∴∠AOC=∠COE﹣∠AOE=90°﹣26°=64°,
∵∠AOC=∠BOD,
∴∠BOD=64°,
又∵OF平分∠BOD,
∴∠DOF=![]() ∠BOD=
∠BOD=![]() ×64°=32°,
×64°=32°,
∴∠COF=180°﹣∠DOF=180°﹣32°=148°=148°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】有这样一道题“计算:(2m4-4m3n-2m2n2)-(m4-2m2n2)+(-m4+4m3n-n3)的值,其中![]() ,n=-1.”小强不小心把
,n=-1.”小强不小心把![]() 错抄成了
错抄成了![]() ,但他的计算结果却也是正确的,你能说出这是为什么吗?
,但他的计算结果却也是正确的,你能说出这是为什么吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A、O、B三点在同一条直线上,OD平分∠AOC,OE平分∠BOC.
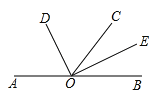
(1)若∠BOC=62°,求∠DOE的度数;
(2)若∠BOC=a°,求∠DOE的度数;
(3)图中是否有互余的角?若有请写出所有互余的角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-(2k+3)x+k2=0有两个不相等的实数根x1,x2.
(1)求k的取值范围;
(2)若两不相等的实数根满足![]() -
-![]() -
-![]() =-9,求实数k的值.
=-9,求实数k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A与点B关于x轴对称,若点A的坐标为(2,3),则点B所在的象限是( )
A.第一象限B.第二象限C.第三象限D.第四象限
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后缷完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,现有以下4个结论: ①快递车从甲地到乙地的速度为100千米/时;
②甲、乙两地之间的距离为120千米;
③图中点B的坐标为(3 ![]() ,75);
,75);
④快递车从乙地返回时的速度为90千米/时,
以上4个结论正确的是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,E是AD的中点,EF⊥AC交CB的延长线于点F.
(1)DE和BF相等吗?请说明理由.
(2)连接AF、BE,四边形AFBE是平行四边形吗?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:a、b、c满足 ![]() 求:
求:
(1)a、b、c的值;
(2)试问以a、b、c为边能否构成三角形?若能构成三角形,求出三角形的周长;若不能构成三角形,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com