【题目】一名快递员骑电动车从饭店出发送外卖，向东走了2千米到达小红家，继续向东走了3.5千米到达小明家，然后又向西走了7.5千米到达小刚家，最后回到饭店．以饭店为原点，以向东的方向为正方向，用一个单位长度表示1千米，点O、A、B、C分别表示饭店、小红家、小明家和小刚家．
（1）请你画出数轴，并在数轴上表示出点O，A，B，C的位置；
（2）小刚家距小红家多远？
（3）若小红步行到小明家每小时走5千米；小刚骑自行车到小明家每小时骑12千米，
若两个人同时分别从自己家出发，问两个人能否同时到达小明家，若不能同时，谁先到达？
【答案】（1）数轴见解析；（2）4千米；（3）小刚先到小明家.
【解析】
（1）根据已知，以饭店为原点，以向东为正方向，用1个单位长度表示1千米快递员骑电动车从饭店出发，向东走了2千米，到达小红家，继续向东走了3.5千米到达小明家，然后西走了7.5千米，到达小刚家，最后返回百货大楼，则小红家、小明家和小刚家在数轴上的位置可知．画出数轴，根据题意在数轴上表示出点O，A，B，C的位置即可；
（2）由（1）得，小红家在饭店东2千米处，小刚家在饭店本2千米处，从而可求出小刚家与小红家的距离；
（3）分别计算出两人所用时间，再进行比较，即可得答案．
（1）点O，A，B，C的位置如图所示：
；
（2）∵|OC|=2，|OA|=2，
∴|AC|=2+2=4，
即小刚家距小红家有4 千米；
（3）两个人不能同时到达小明家.
∵小红家距小明家3.5千米，
∴小红步行到小明家用时为：3.5÷5=0.7（小时）；
∵小刚家距小明家7.5千米，
∴小红步行到小明家用时为：7.5÷12=0.625（小时），
∵0.625小时＜0.7小时，
∴小刚先到小明家.
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】【探究证明】
(1)在矩形ABCD中，EF⊥GH，EF分别交AB，CD于点E，F，GH分别交AD，BC于点G，H.，求证：
；
【结论应用】
(2)如图2，在满足(1)的条件下，又AM⊥BN，点M，N分别在边BC，CD上．若
，求
；
【联系拓展】
(3)如图3，四边形ABCD中，∠ABC＝90°，AB＝AD＝10，BC＝CD＝5，AM⊥DN，点M，N分别在边BC，AB上，求
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了迎接“五·一”小长假的购物高峰，某运动品牌服装专卖店准备购进甲、乙两种服装，甲种服装每件进价l80元，售价320元；乙种服装每件进价l50元，售价280元．
(1)若该专卖店同时购进甲、乙两种服装共200件，恰好用去32400元，求购进甲、乙两种服装各多少件?
(2)该专卖店为使甲、乙两种服装共200件的总利润(利润=售价一进价)不少于26700元， 且不超过26800元，则该专卖店有几种进货方案?
(3)在(2)的条件下，专卖店准备在5月1日当天对甲种服装进行优惠促销活动，决定对甲种服装每件优惠a(0<a<20)元出售，乙种服装价格不变．那么该专卖店要获得最大利润应如何进货?
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在解决数学问题的过程中，我们常用到“分类讨论”的数学思想，下面是运用分类讨论的数学思想解决问题的过程，请仔细阅读，并解答题目后提出的“探究”.
（提出问题）三个有理数a，b，c，满足
，求
的值.
（解决问题）.
解：由题意得，a，b，c三个有理数都为正数或其中一个为正数，另两个为负数.
①当a，b，c都是正数，即
，
，
时，则
（备注：一个非零数除以它本身等于1，如
，则
，
）
②当a，b，c有一个为正数，另两个为负数时，设，
，
，
则
.
（备注：一个非零数除以它的相反数等于-1，如：
，则
）.
所以的值为3或一1.
（探究）请根据上面的解题思路解答下面的问题：
（1）三个有理数a，b，c满足
，求的值；
（2）已知
，
，且
，求
的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知命题“若 a＞b，则 a2＞b2”．
（1）此命题是真命题还是假命题？若是真命题，请给予证明；若是假命题，请举出一个 反例．
（2）写出此命题的逆命题，并判断此逆命题的真假；若是真命题，请给予证明；若是假 命题，请举出一个反例．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图中的虚线网格我们称为正三角形网格，它的每一个小三角形都是边长为 1个单位长度的正三角形，这样的三角形称为单位正三角形．
（1）图①中，已知四边形 ABCD 是平行四边形，求△ABC 的面积和对角线 AC 的长；
（2）图②中，求四边形 EFGH 的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某公司计划投入50万元，开发并生产甲乙两种产品，根据市场调查预计甲产品的年获利y1（万元）与投入资金x（万元）成正比例，乙产品的年获利y2（万元）与投入资金x（万元）的平方成正比例，设该公司投入乙产品x（万元），两种产品的年总获利为y万元（x≥0），得到了表中的数据．
x（万元） | 20 | 30 |
y（万元） | 10 | 13 |
（1）求y与x的函数关系式；
（2）该公司至少可获得多少利润？请你利用所学的数学知识对该公司投入资金的分配提出合理化建
议，使他能获得最大利润，并求出最大利润是多少？
（3）若从年总利润扣除投入乙产品资金的a倍（a≤1）后，剩余利润随x增大而减小，求a的取值
范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在Rt△ABC中，∠C=90°，AC=1cm，BC=2cm，点P从点A出发，以1cm/s的速度沿折线AC→CB→BA运动，最终回到点A，设点P的运动时间为x（s），线段AP的长度为y（cm），则能够反映y与x之间函数关系的图象大致是（ ）
A. 
B. 
C. 
D.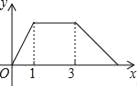 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读理解：如图①，若线段AB在数轴上，A、B两点表示的数分别为
和
(
），则线段AB的长（点A到点B的距离）可表示为AB=
.
请用上面材料中的知识解答下面的问题:如图②，一个点从数轴的原点开始，先向左移动2cm到达P点，再向右移动7cm到达Q点，用1个单位长度表示1cm．
（1）请你在图②的数轴上表示出P，Q两点的位置；
（2）若将图②中的点P向左移动
cm，点Q向右移动
cm，则移动后点P、点Q表示的数分别为多少？并求此时线段PQ的长.（用含的代数式表示）；
（3）若P、Q两点分别从第⑴问标出的位置开始，分别以每秒2个单位和1个单位的速度同时向数轴的正方向运动，设运动时间为
（秒），当为多少时PQ=2cm？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com