
����Ŀ��Ϊ��ӭ�ӡ��塤һ��С���ٵĹ���߷壬ij�˶�Ʒ�Ʒ�װר�����������ס������ַ�װ�����ַ�װÿ������l80Ԫ���ۼ�320Ԫ�����ַ�װÿ������l50Ԫ���ۼ�280Ԫ��
(1)����ר����ͬʱ�����ס������ַ�װ��200����ǡ����ȥ32400Ԫ�����ס������ַ�װ�����ټ�?
(2)��ר����Ϊʹ�ס������ַ�װ��200����������(����=�ۼ�һ����)������26700Ԫ�� �Ҳ�����26800Ԫ�����ר�����м��ֽ�������?
(3)��(2)�������£�ר��������5��1������Լ��ַ�װ�����Żݴ�����������Լ��ַ�װÿ���Ż�a(0<a<20)Ԫ���ۣ����ַ�װ�۸䣮��ô��ר����Ҫ����������Ӧ��ν���?
���𰸡���1�������ס������ַ�װ80����120����2������11�ַ�����3���������ַ�װ70�������ַ�װ130��
���������⣺��1���蹺�����ַ�װx���������ַ�װ�ǣ�200��x������
��������ã�180x��150��200��x��=32400��
��ã�x=80��200��x=200��80=120��
�������ס������ַ�װ80����120����
��2���蹺�����ַ�װy���������ַ�װ�ǣ�200��y��������������ã�
 ����ã�70��y��80��
����ã�70��y��80��
��y����������������11�ַ�����
��3����������ΪWԪ����W=��140��a��y+130��200��y������w=��10��a��y+26000��
����0��a��10ʱ��10��a��0��W��y���������
����y=80ʱ��W�����ֵ����ʱ�������ַ�װ80�������ַ�װ120����
����a=10ʱ����2�������з���������ͬ���������ַ������������ԡ�
����10��a��20ʱ��10��a��0��W��y�������С��
����y=70ʱ��W�����ֵ����ʱ�������ַ�װ70�������ַ�װ130����
��1���蹺�����ַ�װx���������ַ�װ�ǣ�200��x�������������ַ�װ����ȥ32400Ԫ�������г����̣��Ӷ������
��2���蹺�����ַ�װy���������ַ�װ�ǣ�200��y��������������������=�ۼ�-���ۣ�������26700Ԫ���Ҳ�����26800Ԫ�����ɵõ�һ������y�IJ���ʽ�飬�ⲻ��ʽ�鼴�����y�ķ�Χ���ٸ���y���������������������
��3���������������W�ı���ʽ��Ȼ�����a�IJ�ͬȡֵ��Χ�������ۣ��ֱ�ȷ�������������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڼ״����Ҵ����һ����·����C����Ҫ���ƣ���֪��C�빫·�ϵ�ͣ��վA�ľ���Ϊ300�ף��빫·�ϵ���һͣ��վB�ľ���Ϊ400�ף���CA��CB����ͼ��ʾ��Ϊ�˰�ȫ��������Ƶ�C��Χ�뾶250��Χ�ڲ��ý��룬���ڽ��б���ʱ����·AB���Ƿ���Σ�գ�������ѧ����֪ʶ���Խ��.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
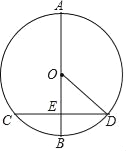
����Ŀ����ͼ���ڡ�O�У�ABΪֱ������AB��CD������ΪE��CD=![]() ��AE=5��
��AE=5��
��1�����O�뾶r��ֵ��
��2����F��ֱ��AB�ϣ�����CF������FCD=![]() ��DOBʱ��ֱ��д��EF�ij�������ͼ�б��F��ľ���λ�ã�
��DOBʱ��ֱ��д��EF�ij�������ͼ�б��F��ľ���λ�ã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
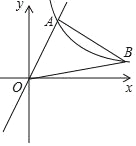
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������A��˫����y=![]() ��x��0��ͬʱ������B���ҵ�A�ڵ�B����࣬��A�ĺ�����Ϊ1����AOB=��OBA=45������k��ֵΪ_____��
��x��0��ͬʱ������B���ҵ�A�ڵ�B����࣬��A�ĺ�����Ϊ1����AOB=��OBA=45������k��ֵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ������1��2��3��4��x��ƽ��������λ����ͬ����ʵ��x��ֵ������![]() ��( )
��( )
A. 0 B. 2.5 C. 3 D. 5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC����ABΪֱ����ԲO���ֱ�BC�ڵ�D����CA���ӳ����ڵ�E������D��DH��AC�ڵ�H������DE���߶�OA�ڵ�F��
��1����֤��DH��ԲO�����ߣ�
��2����AΪEH���е㣬��![]() ��ֵ��
��ֵ��
��3����EA=EF=1����ԲO�İ뾶��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��B��C�������ϱ�ʾ�����ֱ�Ϊa��b��c����OA+OB=OC�������н����У�
��abc��0����a��b+c����0����a��c=b����![]() ��
��
![]()
������ȷ�ĸ����� ��������
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
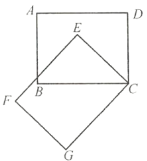
����Ŀ����ͼ��������![]() �Ƶ�
�Ƶ�![]() ����ʱ�뷽����ת
����ʱ�뷽����ת![]() ��õ�ͼ��
��õ�ͼ��![]() .��ش��������⣺
.��ش��������⣺
��1����![]() �Ķ�Ӧ���ǵ�______���߶�
�Ķ�Ӧ���ǵ�______���߶�![]() �Ķ�Ӧ�߶���______��
�Ķ�Ӧ�߶���______��![]() �Ķ�Ӧ����______��
�Ķ�Ӧ����______��
��2����ת������______��![]() �Ĵ�С��______���ı���
�Ĵ�С��______���ı���![]() ����״��______��
����״��______��
��3�����߶�![]() ��ȵ��߶���______.
��ȵ��߶���______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ��2016��6�·ݵ��������У������������������������ڵ��������������ĺͲ�������(�� ��)

A. 27 B. 51 C. 69 D. 72
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com