
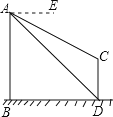
【题目】如图,AB、CD为两个建筑物,建筑物AB的高度为100米,从建筑物AB的顶点A处测得建筑物CD的顶部C处的俯角∠EAC为30°,测得建筑物CD的底部D处的俯角∠EAD为45°.
(1)求两建筑物底部之间水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号).
【答案】(1)两建筑物底部之间水平距离BD的长度为100米;(2)建筑物CD的高度为(100-![]() )米.
)米.
【解析】
(1)根据题意得:BD∥AE,从而得到∠BAD=∠ADB=45°,利用BD=AB=100,求得两建筑物底部之间水平距离BD的长度为100米;
(2)延长AE、DC交于点F,根据题意得四边形ABDF为正方形,根据AF=BD=DF=100,在Rt△AFC中利用∠FAC=30°求得CF,然后即可求得CD的长.
解:(1)根据题意得:BD∥AE,
∴∠ADB=∠EAD=45°,
∵∠ABD=90°,
∴∠BAD=∠ADB=45°,
∴BD=AB=100米,
答:两建筑物底部之间水平距离BD的长度为100米;
(2)延长AE、DC交于点F,根据题意得四边形ABDF为正方形,
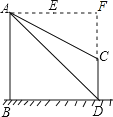
∴AF=BD=DF=100米,
在Rt△AFC中,∠FAC=30°,
∴CF=AFtan∠FAC=100×![]() =
=![]() 米,
米,
又∵FD=100米,
∴CD=10-![]() (米).
(米).
答:建筑物CD的高度为(100-![]() )米.
)米.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】国家为了实现2020年全面脱贫目标,实施“精准扶贫”战略,采取异地搬迁,产业扶持等措施.使贫困户的生活条件得到改善,生活质量明显提高.某旗县为了全面了解贫困县对扶贫工作的满意度情况,进行随机抽样调查,分为四个类别:A.非常满意;B.满意;C.基本满意;D.不满意.依据调查数据绘制成图1和图2的统计图(不完整).
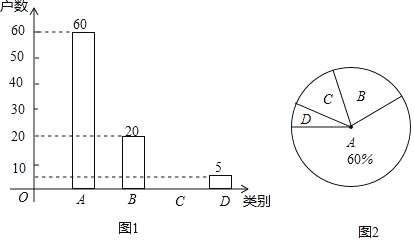
根据以上信息,解答下列问题:
(1)将图1补充完整;
(2)通过分析,贫困户对扶贫工作的满意度(A、B、C类视为满意)是 ;
(3)市扶贫办从该旗县甲乡镇3户、乙乡镇2户共5户贫困户中,随机抽取两户进行满意度回访,求这两户贫困户恰好都是同一乡镇的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
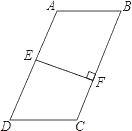
【题目】如图,在四边形ABCD中,AB∥DC,E是AD中点,EF⊥BC于点F,BC=5,EF=3.
(1)若AB=DC,则四边形ABCD的面积S=__;
(2)若AB>DC,则此时四边形ABCD的面积S′__S(用“>”或“=”或“<”填空).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个四边形的一条对角线把四边形分成两个等腰三角形,我们把这条对角线叫这个四边形的和谐线,这个四边形叫做和谐四边形.如菱形就是和谐四边形.
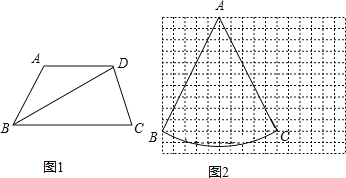
(1)如图1,在梯形ABCD中,AD∥BC,∠BAD=120°,∠C=75°,BD平分∠ABC.求证:BD是梯形ABCD的和谐线;
(2)如图2,在12×16的网格图上(每个小正方形的边长为1)有一个扇形BAC,点A.B.C均在格点上,请在答题卷给出的两个网格图上各找一个点D,使得以A、B、C、D为顶点的四边形的两条对角线都是和谐线,并画出相应的和谐四边形;
(3)四边形ABCD中,AB=AD=BC,∠BAD=90°,AC是四边形ABCD的和谐线,求∠BCD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】华为瓦特实验室试验一种新型快充电池,充电时电池的电量![]() 是充电时间
是充电时间![]() (分
(分![]() 的一次函数,其中
的一次函数,其中![]() .已知充电前电量为
.已知充电前电量为![]() ,测得充电10分钟后电量达到
,测得充电10分钟后电量达到![]() ,充满电后手机马上开始连续工作,工作阶段电池电盘
,充满电后手机马上开始连续工作,工作阶段电池电盘![]() 是工作时间
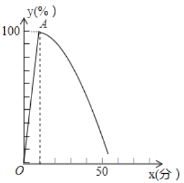
是工作时间![]() 的二次函数,如图所示,
的二次函数,如图所示,![]() 是该二次函数顶点,又测得充满电后连续工作了40分钟,这时电量降为
是该二次函数顶点,又测得充满电后连续工作了40分钟,这时电量降为![]() ,厂商规定手机充电时不能工作,电量小于
,厂商规定手机充电时不能工作,电量小于![]() 时手机部分功能将被限制,不能正常工作.
时手机部分功能将被限制,不能正常工作.
(1)求充电时和充电后使用阶段![]() 关于
关于![]() 的函数表达式(不用写出取值范围);
的函数表达式(不用写出取值范围);
(2)为获得更多实验数据,实验室计划在首次充满电并使用40分钟后停止工作再次充电,充电6分钟后再次工作,假定所有的实验条件不变请问第二次工作的时间多长(电量到![]() 就停止工作)?
就停止工作)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,四边形PDEF是矩形,
,四边形PDEF是矩形,![]() ,
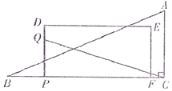
,![]() .矩形PDEF从点B出发,沿射线BC以每秒1个单位长度的速度向点C运动,同时点Q从点P出发,沿折线P-D-E以每秒1个单位长度的速度匀速运动,当点Q到达点E时,点Q与矩形PDEF同时停止运动,连接QC,设点Q的运动时间为t秒(
.矩形PDEF从点B出发,沿射线BC以每秒1个单位长度的速度向点C运动,同时点Q从点P出发,沿折线P-D-E以每秒1个单位长度的速度匀速运动,当点Q到达点E时,点Q与矩形PDEF同时停止运动,连接QC,设点Q的运动时间为t秒(![]() ).
).
(1)求线段PC的长(用含t的代数式表示);
(2)当点Q落在AB边上时,求t的值;
(3)设![]() 的面积为S,求S与t之间的函数关系式;
的面积为S,求S与t之间的函数关系式;
(4)当四边形PDEF与![]() 重叠部分图形为五边形时,直接写出使
重叠部分图形为五边形时,直接写出使![]() 为直角三角形时t的取值范围.
为直角三角形时t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com