
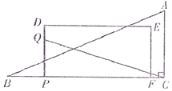
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,四边形PDEF是矩形,
,四边形PDEF是矩形,![]() ,
,![]() .矩形PDEF从点B出发,沿射线BC以每秒1个单位长度的速度向点C运动,同时点Q从点P出发,沿折线P-D-E以每秒1个单位长度的速度匀速运动,当点Q到达点E时,点Q与矩形PDEF同时停止运动,连接QC,设点Q的运动时间为t秒(
.矩形PDEF从点B出发,沿射线BC以每秒1个单位长度的速度向点C运动,同时点Q从点P出发,沿折线P-D-E以每秒1个单位长度的速度匀速运动,当点Q到达点E时,点Q与矩形PDEF同时停止运动,连接QC,设点Q的运动时间为t秒(![]() ).
).
(1)求线段PC的长(用含t的代数式表示);
(2)当点Q落在AB边上时,求t的值;
(3)设![]() 的面积为S,求S与t之间的函数关系式;
的面积为S,求S与t之间的函数关系式;
(4)当四边形PDEF与![]() 重叠部分图形为五边形时,直接写出使
重叠部分图形为五边形时,直接写出使![]() 为直角三角形时t的取值范围.
为直角三角形时t的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)①当
;(3)①当![]() 时,
时,![]() ,②当
,②当![]() 时,
时,![]() ;(4)当
;(4)当![]() 或
或![]() 时,
时,![]() 是直角三角形.
是直角三角形.
【解析】
(1)根据PC=BC-PB计算即可;
(2)当Q落在AB边上时,根据DM+PM=4,构建方程即可解决问题;
(3)分两种情形①当0<t≤4时;②当4<t<12时,分别求解即可解决问题;
(4)分三种情形分别讨论求解,①当点E在AB上时;②如当点Q在线段AC上时;③当![]() 时,∠PQC=90°时.
时,∠PQC=90°时.
(1)![]()
(2)如图①中,
当Q落在AB边上时,DM+PM=4,
∵PM=![]() t,DM=
t,DM=![]() (t-4),
(t-4),
∴![]() t+
t+![]() (t-4)=4,
(t-4)=4,
解得![]() ;
;
(3)①当![]() 时,
时,![]() ;
;
②当![]() 时,
时,![]() ;
;
(4)如图①,当点E在AB上时,
![]() ,
,![]() ,即
,即![]() ,
,
![]() ,
,![]() ,
,
当![]() 时,点Q在线段PD上,此时
时,点Q在线段PD上,此时![]() ,
,
![]() 是直角三角形.
是直角三角形.
如图②,当点Q在线段AC上时,![]() ,
,
此时![]() 是直角三角形,
是直角三角形,![]() ,
,
解得![]() .
.
当![]() 时,若
时,若![]() ,则
,则![]() ,
,
![]() ,
,
整理,得![]() ,
,![]() ,
,
![]() 此种情况不存在.
此种情况不存在.
综上所述,当![]() 或
或![]() 时,
时,![]() 是直角三角形.
是直角三角形.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
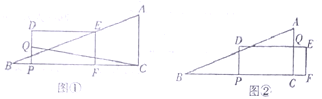
【题目】在同一平面直角坐标系中,一次函数![]() 与反比例函数
与反比例函数![]() (
(![]() 为常数,且
为常数,且![]() )的图像交于
)的图像交于![]() 、
、![]() 两点,它们的部分图像如图所示,
两点,它们的部分图像如图所示,![]() 的面积是6.
的面积是6.
(1)求一次函数![]() 与反比例函数
与反比例函数![]() 的表达式;
的表达式;
(2)请直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
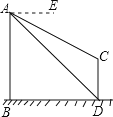
【题目】如图,AB、CD为两个建筑物,建筑物AB的高度为100米,从建筑物AB的顶点A处测得建筑物CD的顶部C处的俯角∠EAC为30°,测得建筑物CD的底部D处的俯角∠EAD为45°.
(1)求两建筑物底部之间水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
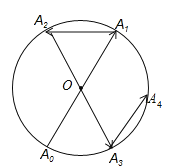
【题目】如图所示,一动点从半径为2的![]() 上的
上的![]() 点出发,沿着射线
点出发,沿着射线![]() 方向运动到
方向运动到![]() 上的点
上的点![]() 处,再向左沿着与射线
处,再向左沿着与射线![]() 夹角为
夹角为![]() 的方向运动到
的方向运动到![]() 上的点
上的点![]() 处;接着又从
处;接着又从![]() 点出发,沿着射线
点出发,沿着射线![]() 方向运动到
方向运动到![]() 上的点
上的点![]() 处,再向左沿着与射线
处,再向左沿着与射线![]() 夹角为
夹角为![]() 的方向运动到
的方向运动到![]() 上的点
上的点![]() 处;
处;![]() 间的距离是________;…按此规律运动到点
间的距离是________;…按此规律运动到点![]() 处,则点
处,则点![]() 与点
与点![]() 间的距离是________.
间的距离是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某市的一幢在建的楼,准备上市销售,该楼前有一座装有高压线的铁塔BC经过,市民想知道高压线的电辐射对居住是否有影响,则需要测量该楼到铁塔的水平距离DC的长以及铁塔BC的高度.为了安全,不能直接测量铁塔的高度.在该楼的楼顶A处测得铁塔的塔B的仰角过![]() ,测得铁塔的塔底C的俯角
,测得铁塔的塔底C的俯角![]() ,该楼的高度
,该楼的高度![]() ,求铁塔BC的高度(参考数据:
,求铁塔BC的高度(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ).
).

查看答案和解析>>
科目:初中数学 来源: 题型:
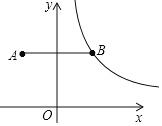
【题目】在平面直角坐标系中,点A(-2,3)关于y轴的对称点为点B,连接AB,反比例函数y=![]() (x>0)的图象经过点B,过点B作BC⊥x轴于点C,点P是该反比例函数图象上任意一点.
(x>0)的图象经过点B,过点B作BC⊥x轴于点C,点P是该反比例函数图象上任意一点.
(1)求k的值;
(2)若△ABP的面积等于2,求点P坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年春节期间,兰州市开展了以“精致兰州志愿同行”为主题的系列志愿服务活动.金老师和程老师积极参加志愿者活动,当时有下列四个志愿者工作岗位供他们选择:
①“送温暖”活动岗位:为困难家庭打扫卫生,为留守儿童提供学业辅导;(分别用![]() ,
,![]() 表示)
表示)
②“送平安”活动岗位:消防安全常识宣传,人员密集场所维护秩序.(分别用![]() ,
,![]() 表示)
表示)
(1)金老师从四个岗位中随机选取一个报名,恰好选择“送温暖”活动岗位的概率是多少?
(2)若金老师和程老师各随机从四个活动岗位中选一个报名,请用树状图或列表法求出他们恰好都选择同一个岗位的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:当前,中国互联网产业发展迅速,互联网教育市场增长率位居全行业前列.以下是根据某媒体发布的2012﹣2015年互联网教育市场规模的相关数据,绘制的统计图表的一部分.
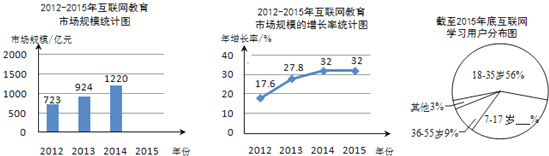
(1)2015年互联网教育市场规模约是 亿元(结果精确到1亿元),并补全条形统计图;
(2)截至2015年底,约有5亿网民使用互联网进行学习,互联网学习用户的年龄分布如图所示,请你补全扇形统计图,并估计7﹣17岁年龄段有 亿网民通过互联网进行学习;
(3)根据以上材料,写出你的思考、感受或建议(一条即可).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com