
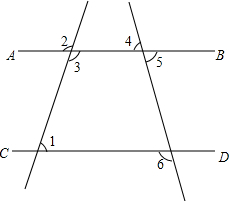
 已知|3m-2n+60|与(7m-3n-60)2互为相反数,且m、n的值分别是图中∠1与∠2的度数,如果∠4=70°,试求∠6的度数.
已知|3m-2n+60|与(7m-3n-60)2互为相反数,且m、n的值分别是图中∠1与∠2的度数,如果∠4=70°,试求∠6的度数. 分析 首先根据非负数的性质可得$\left\{\begin{array}{l}{3m-2n+60=0}\\{7m-3n-60=0}\end{array}\right.$,解方程组可得$\left\{\begin{array}{l}{m=60}\\{n=120}\end{array}\right.$,进而可得∠1=60°,∠2=120°,然后再根据同旁内角互补,两直线平行可得AB∥CD,再根据平行线的性质可得答案.
解答 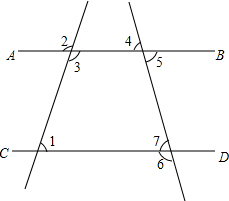 解:∵|3m-2n+60|与(7m-3n-60)2互为相反数,
解:∵|3m-2n+60|与(7m-3n-60)2互为相反数,
∴$\left\{\begin{array}{l}{3m-2n+60=0}\\{7m-3n-60=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=60}\\{n=120}\end{array}\right.$,
∴∠1=60°,∠2=120°,
∵∠2=∠3,
∴∠3=120°,
∴∠1+∠3=180°,
∴AB∥CD,
∴∠4=∠7=70°,
∴∠6=110°.
点评 此题主要考查了平行线的判定和性质,以及解二元一次方程组,非负数的性质,关键是掌握绝对值和偶次幂都具有非负性.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
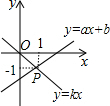 已知函数y=ax+b与函数y=kx的图象相交于点P,根据图象,可得关于x、y的二元一次方程组$\left\{\begin{array}{l}{ax-y+b=0}\\{kx-y=0}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$.
已知函数y=ax+b与函数y=kx的图象相交于点P,根据图象,可得关于x、y的二元一次方程组$\left\{\begin{array}{l}{ax-y+b=0}\\{kx-y=0}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 20%x-30=900×80%-x | B. | 20%x=900×80%-30-x | ||
| C. | 900×20%=900×80%-x-30 | D. | 900×20%=900×80%+30-x |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
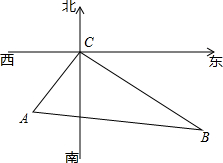 在寻找马航MH370航班过程中,A、B两艘舰艇分别沿东北方向和西北方向航行,两艘搜救舰艇接到命令后同时出发,A舰艇的速度为24海里/时,B舰艇的速度为32海里/时,经过2小时,它们同时到达事故发生的地点C,求A、B两艘舰艇在出发时相距多远?
在寻找马航MH370航班过程中,A、B两艘舰艇分别沿东北方向和西北方向航行,两艘搜救舰艇接到命令后同时出发,A舰艇的速度为24海里/时,B舰艇的速度为32海里/时,经过2小时,它们同时到达事故发生的地点C,求A、B两艘舰艇在出发时相距多远?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com