
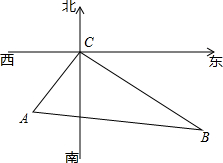
 在寻找马航MH370航班过程中,A、B两艘舰艇分别沿东北方向和西北方向航行,两艘搜救舰艇接到命令后同时出发,A舰艇的速度为24海里/时,B舰艇的速度为32海里/时,经过2小时,它们同时到达事故发生的地点C,求A、B两艘舰艇在出发时相距多远?
在寻找马航MH370航班过程中,A、B两艘舰艇分别沿东北方向和西北方向航行,两艘搜救舰艇接到命令后同时出发,A舰艇的速度为24海里/时,B舰艇的速度为32海里/时,经过2小时,它们同时到达事故发生的地点C,求A、B两艘舰艇在出发时相距多远?  阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | ($\frac{2}{3}$)2与$\frac{{2}^{2}}{3}$ | B. | -22与(-2)2 | C. | -(-1)2011与(-1)2010 | D. | (-5)2与-52 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
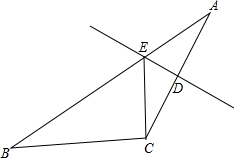 如图,△ABC中,边AC的垂直平分线分别交AB、AC于点E、D,若AE=6.
如图,△ABC中,边AC的垂直平分线分别交AB、AC于点E、D,若AE=6.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com