
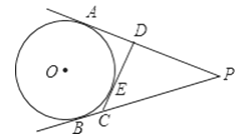
【题目】如图,PA、PB切⊙O于A、B两点,CD切⊙O于点E,分别交PA、PB于点C、D.若PA、PB的长是关于x的一元二次方程x2﹣mx+m﹣1=0的两个根,求△PCD的周长.
【答案】2
【解析】
由PA、PB切⊙O于A、B两点,CD切⊙O于点E,根据切线长定理,可得PA=PB,又由PA、PB的长是关于x的一元二次方程x2﹣mx+m﹣1=0的两个根,根据根与系数的关系,可求得PA与PB的长,又由CD切⊙0于点E,即可得△PCD的周长等于PA+PB.
解:∵PA、PB的长是关于x的一元二次方程x2﹣mx+m﹣1=0的两个根,
∴PA+PB=m,PAPB=m﹣1,
∵PA、PB切⊙O于A、B两点,
∴PA=PB=![]() ,
,
即![]()
![]() =m﹣1,
=m﹣1,
即m2﹣4m+4=0,
解得:m=2,
∴PA=PB=1,
∵PA、PB切⊙O于A、B两点,CD切⊙O于点E,
∴AD=ED,BC=EC,
∴△PCD的周长为:PD+CD+PC=PD+DE+EC+PC=PD+AD+BC+PC=PA+PB=2.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
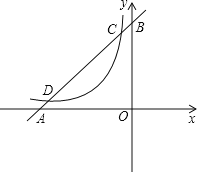
【题目】如图,直线y1=x+m与x轴、y轴交于点A、B,与双曲线![]() 分别交于点C、D,且点C的坐标为(-1,2)
分别交于点C、D,且点C的坐标为(-1,2)
(1)分别求出直线AB及双曲线的解析式;
(2)求出点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
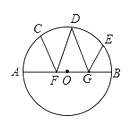
【题目】如图,在⊙O中,F,G是直径AB上的两点,C,D,E是半圆上的三点,如果弧AC的度数为60°,弧BE的度数为20°,∠CFA=∠DFB,∠DGA=∠EGB.求∠FDG的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
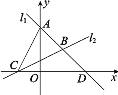
【题目】如图,直线l1过点A(0,4)与点D(4,0),直线l2:y=![]() x+1与x轴交于点C,两直线l1,l2相交于点B.
x+1与x轴交于点C,两直线l1,l2相交于点B.
(1)求直线l1的函数表达式;
(2)求点B的坐标;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
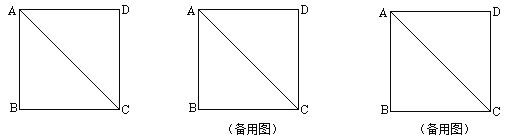
【题目】操作:将一把三角尺放在边长为1的正方形ABCD上,并使它的直角顶点P在对角线AC上滑动,直角的一边始终经过点B,另一边与射线DC相交于点Q,设A、P两点间的距离为x.
探究:
(1)当点Q在边CD上时,线段PQ与线段PB之间有怎样的大小关系?试证明你观察到的结论;
(2)当点Q在边CD上时,设四边形PBCQ的面积为y,求y与x之间的函数关系式,并写出x的取值范围;(3)当点P在线段AC上滑动时,△PCQ是否能成为等腰三角形?如果可能,指出所有能使△PCQ成为等腰三角形的点Q的位置,并求出相应x的值;如果不可能,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F.
(1)试判断直线BC与⊙O的位置关系,并说明理由;
(2)若BD=2![]() ,BF=2,求阴影部分的面积(结果保留π).
,BF=2,求阴影部分的面积(结果保留π).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)为弘扬 “东亚文化”,某单位开展了“东亚文化之都”演讲比赛,在安排1位女选手和3位男选手的出场顺序时,采用随机抽签方式.
(1)请直接写出第一位出场是女选手的概率;
(2)请你用画树状图或列表的方法表示第一、二位出场选手的所有等可能结果,并求出他们都是男选手的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,并完成相应的任务.
基本性质:三角形中线等分三角形的面积.
如图,![]() 是
是![]() 的边
的边![]() 上的中线,
上的中线,
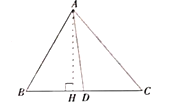
则![]()
理由:过点![]() 作
作![]() 于点
于点![]()
∵![]() 是
是![]() 的边
的边![]() 上的中线.
上的中线.
∴![]() 又∵
又∵![]() ,
,![]()
∴![]()
∴三角形中线等分三角形的面积.
任务:
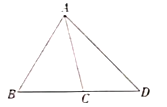
(1)如图,延长![]() 的边
的边![]() 到点
到点![]() ,使
,使![]() ,连接
,连接![]() ,则
,则![]() 和
和![]() 的数量关系为_________.
的数量关系为_________.
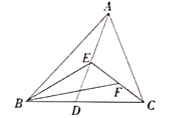
(2)如图,点![]() 是
是![]() 的边
的边![]() 上任意一点,点
上任意一点,点![]() 分别是线段
分别是线段![]() ,
,![]() 的中点,且
的中点,且![]() 的面积为
的面积为![]() ,请同学们借助上述结论求
,请同学们借助上述结论求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com