
【题目】如图,四边形ABCD中,对角线AC与BD相交于点O,在①AB∥CD;②AO=CO;③AD=BC中任意选取两个作为条件,“四边形ABCD是平行四边形”为结论构造命题. 
(1)以①②作为条件构成的命题是真命题吗?若是,请证明;若不是,请举出反例;
(2)写出按题意构成的所有命题中的假命题,并举出反例加以说明.(命题请写成“如果…,那么….”的形式)
【答案】
(1)解:以①②作为条件构成的命题是真命题,
证明:∵AB∥CD,
∴∠OAB=∠OCD,
在△AOB和△COD中,
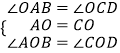 ,
,
∴△AOB≌△COD(ASA),
∴OB=OD,
∴四边形ABCD是平行四边形
(2)解:根据①③作为条件构成的命题是假命题,即如果有一组对边平行,另一组对边相等,那么四边形是平行四边形,如等腰梯形符合,但不是平行四边形; 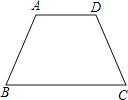
根据②③作为条件构成的命题是假命题,即如果一个四边形ABCD的对角线交于O,且OA=OC,AD=BC,那么这个四边形是平行四边形,如图,
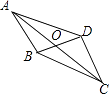
根据已知不能推出OB=OD或AD∥BC或AB=DC,即四边形不是平行四边形.
【解析】(1)根据平行得出全等三角形,即可求出OB=OD,根据平行四边形的判定推出即可;(2)根据等腰梯形和平行四边形的判定判断即可.
【考点精析】本题主要考查了平行四边形的判定和命题与定理的相关知识点,需要掌握两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形;我们把题设、结论正好相反的两个命题叫做互逆命题.如果把其中一个叫做原命题,那么另一个叫做它的逆命题;经过证明被确认正确的命题叫做定理才能正确解答此题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的函数图像与x轴、y轴分别交于点A、B,以线段AB为直角边在第一象限内作Rt△ABC,且使∠ABC=30.
的函数图像与x轴、y轴分别交于点A、B,以线段AB为直角边在第一象限内作Rt△ABC,且使∠ABC=30.
(1)求△ABC的面积;
(2)如果在第二象限内有一点P(m,![]() ),试用含m的代数式表示四边形AOPB的面积,并求当△APB与△ABC面积相等时m的值;
),试用含m的代数式表示四边形AOPB的面积,并求当△APB与△ABC面积相等时m的值;
(3)是否存在使△QAB是等腰三角形并且在坐标轴上的点Q?若存在,请写出Q的所有可能的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中装有白球2个和黄球1个,这些球除颜色外都相同,搅匀后从中任意摸出1个球,记下颜色后不放回,搅匀后再从中任意摸出1个球,请用列表或画树状图的方法求两次都摸出白球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,边AC的垂直平分线交BC于点D,交AC于点E,连接BE. 
(1)若∠C=30°,求证:BE是△DEC外接圆的切线;
(2)若BE= ![]() ,BD=1,求△DEC外接圆的直径.
,BD=1,求△DEC外接圆的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为a的正方形中挖掉一个边长为b的小正方形(a>b).把余下的部分剪拼成一个矩形(如图).通过计算图形(阴影部分)的面积,验证了一个等式,则这个等式是( )
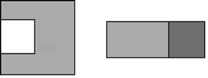
A. a2﹣b2=(a+b)(a﹣b) B. (a+b)2=a2+2ab+b2
C. (a﹣b)2=a2﹣2ab+b2 D. a2﹣ab=a(a﹣b)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD平分∠BAC , 按如下步骤作图:
第一步,分别以点A、D为圆心,以大于 ![]() AD的长为半径在AD两侧作弧,交于两点M、N;
AD的长为半径在AD两侧作弧,交于两点M、N;
第二步,连接MN分别交AB、AC于点E、F;
第三步,连接DE、DF .
若BD=6,AF=4,CD=3,则BE的长是( ).
A.2
B.4
C.6
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解一元二次方程x2-2x-5=0,结果正确的是( )
A.x1=-1+ ![]() ,x2=-1-
,x2=-1- ![]()
B.x1=1+ ![]() ,x2=1-
,x2=1- ![]()
C.x1=7,x2= 5
D.x1= 1+ ![]() ,x2=1-
,x2=1- ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com