【题目】根据条件求二次函数的解析式：
（1）抛物线的顶点坐标为（﹣1，﹣1），且与y轴交点的纵坐标为﹣3
（2）抛物线在x轴上截得的线段长为4，且顶点坐标是（3，﹣2）．
【答案】（1）y=﹣2x2﹣4x﹣3；（2）y=
x2﹣3x+
【解析】试题分析：应用待定系数法，求出每个二次函数的解析式各是多少即可．
试题解析：（1）∵抛物线的顶点坐标为（﹣1，﹣1），
∴设抛物线的解析式为：y=a（x+1）2﹣1，
∵抛物线与y轴交点的纵坐标为﹣3，
∴﹣3=a（0+1）2﹣1，
解得a=﹣2．
∴抛物线的解析式是y=﹣2（x+1）2﹣1，
即y=﹣2x2﹣4x﹣3
（2）∵抛物线的顶点坐标是（3，﹣2），
∴抛物线的对称轴为直线x=3，
∵抛物线在x轴上截得的线段长为4，
∴抛物线与x轴的两交点坐标为（1，0），（5，0），
设抛物线的解析式为y=k（x﹣1）（x﹣5），
则﹣2=k（3﹣1）（3﹣5）
解得k= 
，
∴抛物线解析式为y=
（x﹣1）（x﹣5），
即y=
x2﹣3x+
科目：初中数学 来源： 题型：
【题目】在△ABC 内任取一点 P (如图①)，连接 PB、PC，探索∠BPC 与∠A，∠ABP，∠ACP 之间的数量关系，并证明你的结论：当点 P 在△ABC 外部时 (如图②)，请直接写出∠BPC 与∠A，∠ ABP，∠ACP 之间的数量关系。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，AB为⊙O的直径，点C、D在⊙O上，且BC=6cm，AC=8cm，∠ABD=45°．
（1）求BD的长；
（2）求图中阴影部分的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】解不等式组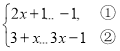
请结合题意填空，完成本题的解答。
（I）解不等式①，得________________
（Ⅱ）解不等式②，得：_____________________
（Ⅲ）把不等式①和②的解集在数轴上表示出来：
（IV）原不等式组的解集为___________________.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（阅读理解）
在解方程组或求代数式的值时，可以用整体代入或整体求值的方法，化难为易．
（1）解方程组
（2）已知
，求x+y+z的值
解：（1）把②代入①得：x+2×1＝3．解得：x＝1．
把x＝1代入②得：y＝0．
所以方程组的解为
，
（2）①×2得：8x+6y+4z＝20．③
②﹣③得：x+y+z＝5．
（类比迁移）
（1）若
，则x+2y+3z＝ ．
（2）解方程组
（实际应用）
打折前，买39件A商品，21件B商品用了1080元．打折后，买52件A商品，28件B商品用了1152元，比不打折少花了多少钱？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一列快车从甲地驶往乙地，一列特快车从乙地驶往甲地，快车的速度为100千米/小时，特快车的速度为150千米/小时，甲乙两地之间的距离为1000千米，两车同时出发，则图中折线大致表示两车之间的距离y（千米）与快车行驶时间t（小时）之间的函数图象是
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在Rt△ABC中，∠ABC＝90°，以AB为直径作半圆⊙O交AC于点D，点E为BC的中点，连接DE.
(1)求证：DE是半圆⊙O的切线；
(2)若∠BAC＝30°，DE＝2，求AD的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知抛物线y=ax﹣2ax＋3(a≠0)，与x轴交于A、B两点，与y轴交于点C，若OB=3OA．
（1）求抛物线的解析式；
（2）连接BC，点P、点Q是第一象限的抛物线上不同的两点，是否存在这样的P点，使得
恒成立？若存在，请求P点的坐标，若不存在，请说明理由；
（3）如图2，D为抛物线的对称轴与x轴的交点，M为线段OC上一点，过点M作直线l交抛物线于E、F两点，连接AE、OE、BF、DF若△AEO∽△DFB，求M点的坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
