如图.已知抛物线y=ax2+bx+c经过A 点.动点D从原点O开始沿OB方向以每秒1个单位长度移动.动点E从点C开始沿CO方向以每秒1个长度单位移动.动点D.E同时出发.当动点E到达原点O时.点D.E停止运动．(1)求抛物线的解析式及顶点P的坐标,.求△DEF的面积S与E点运动时间t的函数解析式,当t为何值时.△DEF的面积最大?最大面积是多少?(3)� 题目和参考答案——青夏教育精英家教网—

1．

如图，已知抛物线y=ax²+bx+c经过A （1，0）、B（0，3）及C（3，0）点，动点D从原点O开始沿OB方向以每秒1个单位长度移动，动点E从点C开始沿CO方向以每秒1个长度单位移动，动点D、E同时出发，当动点E到达原点O时，点D、E停止运动．
（1）求抛物线的解析式及顶点P的坐标；
（2）若F（-1，0），求△DEF的面积S与E点运动时间t的函数解析式；当t为何值时，△DEF的面积最大？最大面积是多少？
（3）当△DEF的面积最大时，抛物线的对称轴上是否存在一点N，使△EBN是直角三角形？若存在，求出N点的坐标，若不存在，请说明理由．

分析（1）根据待定系数法，可得函数解析式，根据配方法，可得顶点坐标；
（2）根据三角形的面积公式，可得函数解析式，根据二次函数的性质，可得答案；
（3）根据勾股定理的逆定理，可得关于a的方程，根据解方程，可得N点坐标．

解答解：（1）将A （1，0）、B（0，3）及C（3，0）代入函数解析式，得
$\left\{\begin{array}{l}{a+b+c=0}\\{9a+3b+c=0}\\{c=3}\end{array}\right.$，
解得$\left\{\begin{array}{l}{a=1}\\{b=-4}\\{c=3}\end{array}\right.$，
抛物线的解析式为y=x²-4x+3，
配方，得y=（x-2）²-1，顶点P的坐标为（2，-1）；
（2）如图1，
由题意，得
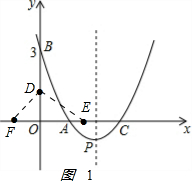CE=t，OE=3-t，FE=4-t，OD=t．
S=$\frac{1}{2}$FE•OD=$\frac{1}{2}$（4-t）t=-$\frac{1}{2}$t²+2t=-$\frac{1}{2}$（t-2）²+2，
当t=2时，S_最大=2；
（3）当△DEF的面积最大时，E（1，0），设N（2，a），
BN²=4+（a-3）²，EN²=1+a²，BE²=1+9=10，
①当BN²+EN²=BE²时，4+9-6a+a²+a²+1=10，化简，得
a²-3a+2=0，解得a=2，a=1，N（2，2），N（2，1）；
②当BN²+BE²=EN²时，4+9-6a+a²+10=1+a²，化简，得
6a=22，解得a=$\frac{11}{3}$，N（2，$\frac{11}{3}$）；
③当BE²+EN²=BN²时，1+a²+10=4+9-6a+a²，
化简，得
6a=2，解得a=$\frac{1}{3}$，N（2，$\frac{1}{3}$），
综上所述：N点的坐标（2，2），（2，1），（2，$\frac{11}{3}$），（2，$\frac{1}{3}$）．

点评本题考查了二次函数综合题，利用待定系数求函数解析式；利用二次函数的性质求面积的最大值；利用勾股定理的逆定理得出关于a的方程是解题关键，要分类讨论，以防遗漏．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>