
【题目】如图,四边形ABCD的对角线相交于点O,且点O是BD的中点,若AB=AD=5,BD=8,∠ABD=∠CDB,则四边形ABCD的面积为( )

A.40B.24C.20D.15
科目:初中数学 来源: 题型:
【题目】阅读下列例题的解题过程,并完成相关问题
例:如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8 cm,AD=12cm,BC=18cm,点P从点A出发,以1cm/s的速度向点D运动;点Q从点C同时出发,以2cm/s的速度向点B运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.从运动开始,使PQ∥CD和PQ=CD,分别经过多长时间?为什么?
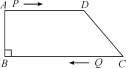
解:①设经过ts时,PQ∥CD且PQ=CD,此时四边形PQCD为平行四边形.
∵PD=(12-t)cm,CQ=2t cm,
∴12-t=2t.∴t=4.
∴当t=4时,PQ∥CD,且PQ=CD.
②设经过ts时,PQ=CD,分别过点P,D作BC边的垂线PE,DF,垂足分别为E,F.
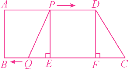
当CF=EQ时,四边形PQCD为梯形(腰相等)或者平行四边形.
∵∠B=∠A=∠DFB=90°,
∴四边形ABFD是矩形.∴AD=BF.
∵AD=12 cm,BC=18 cm,
∴CF=BC-BF=6 cm.
当四边形PQCD为梯形(腰相等)时,
PD+2(BC-AD)=CQ,
∴(12-t)+12=2t.∴t=8.
∴当t=8时,PQ=CD.
当四边形PQCD为平行四边形时,由①知当t=4时,PQ=CD.
综上,当t=4时,PQ∥CD;当t=4或t=8时,PQ=CD.
问题1:在整个运动过程中是否存在t值,使得四边形PQCD是菱形?若存在,请求出t值;若不存在,请说明理由.
问题2:从运动开始,当t取何值时,四边形PQBA是矩形?
问题3:在整个运动过程中是否存在t值,使得四边形PQBA是正方形?若存在,请求出t值;若不存在,请说明理由.
问题4:是否存在t,使得△DQC是等腰三角形?若存在,请求出t值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知FG⊥AB,CD⊥AB,垂足分别为G,D,∠1=∠2,
求证:∠CED+∠ACB=180°,
请你将小明的证明过程补充完整.
证明:∵FG⊥AB,CD⊥AB,垂足分别为G,D(已知)
∴∠FGB=∠CDB=90°( ).
∴GF∥CD( )
∵GF∥CD(已证)
∴∠2=∠BCD( )
又∵∠1=∠2(已知)
∴∠1=∠BCD( )
∴ ( )
∴∠CED+∠ACB=180°( )

查看答案和解析>>
科目:初中数学 来源: 题型:
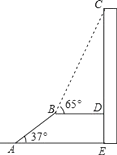
【题目】如图,AB是长为10m,倾斜角为37°的自动扶梯,平台BD与大楼CE垂直,且与扶梯AB的长度相等,在B处测得大楼顶部C的仰角为65°,求大楼CE的高度(结果保留整数).
(参考数据:sin37°≈ ![]() ,tan37°≈
,tan37°≈ ![]() ,sin65°≈
,sin65°≈ ![]() ,tan65°≈
,tan65°≈ ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
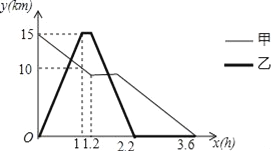
【题目】某森林公园从正门到侧门有一条公路供游客运动,甲徒步从正门出发匀速走向侧门,出发一段时间开始休息,休息了0.6小时后仍按原速继续行走.乙与甲同时出发,骑自行车从侧门匀速前往正门,到达正门后休息0.2小时,然后按原路原速匀速返回侧门.图中折线分别表示甲、乙到侧门的路程y(km)与甲出发时间x(h)之间的函数关系图象.根据图象信息解答下列问题.
(1)求甲在休息前到侧门的路程y(km)与出发时间x(h)之间的函数关系式.
(2)求甲、乙第一次相遇的时间.
(3)直接写出乙回到侧门时,甲到侧门的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,平行四边形OABC的顶点A的坐标为(﹣4,0),顶点B在第二象限,∠BAO=60°,BC交y轴于点D,DB:DC=3:1.若函数y= ![]() (k>0,x>0)的图象经过点C,则k的值为( )
(k>0,x>0)的图象经过点C,则k的值为( )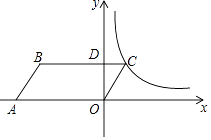
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料;
课堂上,老师设计了一个活动:将一个4×4的正方形网格沿着网格线划分成两部分(分别用阴影和空白表示),使得这两部分图形是全等的,请同学们尝试给出划分的方法.约定:如果两位同学的划分结果经过旋转、翻折后能够重合,那么就认为他们的划分方法相同.
小方、小易和小红分别对网格进行了划分,结果如图①、图②、图③所示.
小方说:“我们三个人的划分方法都是正确的,但是将小红的整个图形(图③)逆时针旋转90![]() 后得到的划分方法与我的划分方法(图①)是一样的,应该认为是同一种方法,而小易的划分方法与我的不同,”
后得到的划分方法与我的划分方法(图①)是一样的,应该认为是同一种方法,而小易的划分方法与我的不同,”
老师说:“小方说得对.”

完成下列问题:
(1)图④的划分方法是否正确?
(2)判断图⑤的划分方法与图②小易的划分方法是否相同,并说明你的理由.
(3)请你再想出一种与已有方法不同的划分方法,使之满足上述条件,并在图⑥中画出来.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在1~7月份,某地的蔬菜批发市场指导菜农生产和销售某种蔬菜,并向他们提供了这种蔬菜每千克售价与每千克成本的信息如图所示,则出售该种蔬菜每千克利润最大的月份可能是( ) 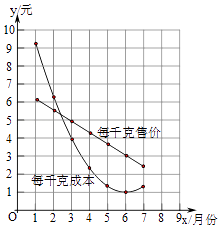
A.1月份
B.2月份
C.5月份
D.7月份
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com