
【题目】阅读下列例题的解题过程,并完成相关问题
例:如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8 cm,AD=12cm,BC=18cm,点P从点A出发,以1cm/s的速度向点D运动;点Q从点C同时出发,以2cm/s的速度向点B运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.从运动开始,使PQ∥CD和PQ=CD,分别经过多长时间?为什么?
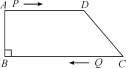
解:①设经过ts时,PQ∥CD且PQ=CD,此时四边形PQCD为平行四边形.
∵PD=(12-t)cm,CQ=2t cm,
∴12-t=2t.∴t=4.
∴当t=4时,PQ∥CD,且PQ=CD.
②设经过ts时,PQ=CD,分别过点P,D作BC边的垂线PE,DF,垂足分别为E,F.
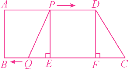
当CF=EQ时,四边形PQCD为梯形(腰相等)或者平行四边形.
∵∠B=∠A=∠DFB=90°,
∴四边形ABFD是矩形.∴AD=BF.
∵AD=12 cm,BC=18 cm,
∴CF=BC-BF=6 cm.
当四边形PQCD为梯形(腰相等)时,
PD+2(BC-AD)=CQ,
∴(12-t)+12=2t.∴t=8.
∴当t=8时,PQ=CD.
当四边形PQCD为平行四边形时,由①知当t=4时,PQ=CD.
综上,当t=4时,PQ∥CD;当t=4或t=8时,PQ=CD.
问题1:在整个运动过程中是否存在t值,使得四边形PQCD是菱形?若存在,请求出t值;若不存在,请说明理由.
问题2:从运动开始,当t取何值时,四边形PQBA是矩形?
问题3:在整个运动过程中是否存在t值,使得四边形PQBA是正方形?若存在,请求出t值;若不存在,请说明理由.
问题4:是否存在t,使得△DQC是等腰三角形?若存在,请求出t值;若不存在,请说明理由.
【答案】问题1:不存在.理由见解析;问题2:当t=6时,四边形PQBA是矩形;问题3:不存在.理由见解析;问题4:当t=5或6或![]() 时,△DQC是等腰三角形.
时,△DQC是等腰三角形.
【解析】
问题1:要使四边形PQCD是菱形,则四边形PQCD一定是平行四边形,由例可知当t=4时,四边形PQCD是平行四边形,而此时DP≠DC,从而可得出结论;
问题2:因为∠B=90°,AP∥BQ,由矩形的判定可知当AP=BQ时,四边形ABQP成为矩形,据此列方程求解即可;
问题3:要使四边形PQBA是正方形,则四边形PQBA一定是矩形.由问题2知当t=6时,四边形PQBA是矩形,而此时AP≠AB,从而可得出结论;
问题4:分三种情况讨论计算,①当QC=DC时;②当DQ=DC时,过点D作DH⊥CQ;③当QD=QC时,过点D作DH⊥CQ,分别列出方程求出时间,判断时间是否符合题意即可.
解:问题1:不存在.理由:
要使四边形PQCD是菱形,则四边形PQCD一定是平行四边形.
由例知当t=4时,四边形PQCD是平行四边形.
此时DP=12-t=8≠10,即DP≠DC,
所以按已知速度运动,四边形PQCD只能是平行四边形,但不可能是菱形.
问题2:如图,由题意,得AP=t,DP=12-t,CQ=2t,BQ=18-2t.
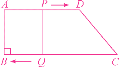
要使四边形PQBA是矩形,已有∠B=90°,AD∥BC,即AP∥BQ,只需满足AP=BQ,即t=18-2t,解得t=6.
所以当t=6时,四边形PQBA是矩形.
问题3:不存在.理由:
要使四边形PQBA是正方形,则四边形PQBA一定是矩形.
由问题2知当t=6时,四边形PQBA是矩形.
此时AP=t=6≠8,即AP≠AB,
所以按已知速度运动,四边形PQBA只能是矩形,但不可能是正方形.
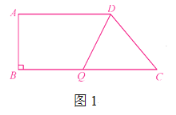
问题4:当△DQC是等腰三角形时,分三种情况:
①如图1,当QC=DC时,即2t=10,∴t=5.
②如图2,当DQ=DC时,过点D作DH⊥CQ,
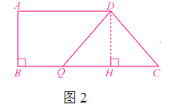
则QH=CH=![]() CQ=t.
CQ=t.
在Rt△DHC中,DH=8,CH=BC-AD=6,
∴DC=![]() =10,
=10,
∴t=6.
③如图3,当QD=QC时,过点D作DH⊥CQ,DH=8,CH=6,DC=10,CQ=QD=2t,QH=2t-6.
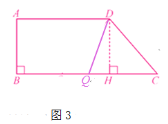
在Rt△DQH中,DH2+QH2=DQ2.
∴82+(2t-6)2=(2t)2.
解得t=![]() .
.
综上,当t=5或6或![]() 时,△DQC是等腰三角形.
时,△DQC是等腰三角形.


科目:初中数学 来源: 题型:
【题目】如图,已知AD∥BC,AB⊥BC,AB=3,点E为射线BC上一个动点,连接AE,将△ABE沿AE折叠,点B落在点B′处,过点B′作AD的垂线,分别交AD,BC于点M,N.当点B′为线段MN的三等分点时,BE的长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年1月重庆湖童时装周在重庆渝北举行了八场走秀,云集了八大国内外潮童品牌,不仅为大家带来了一场品牌走秀盛会,更让人们将目光转移到了![]() 后、
后、![]() 后童模群体身上,开启服装新秀湖流.某大型商场抓住这次商机购进
后童模群体身上,开启服装新秀湖流.某大型商场抓住这次商机购进![]() 两款新童装进行试销售,该商场用
两款新童装进行试销售,该商场用![]() 元购买
元购买![]() 款童装,用
款童装,用![]() 元购买
元购买![]() 款童装,且每件
款童装,且每件![]() 款童装进价与每件
款童装进价与每件![]() 款童装进价相同,购买
款童装进价相同,购买![]() 款童装的数量比
款童装的数量比![]() 款童装的数量少
款童装的数量少![]() 件,若该商场本次以每件
件,若该商场本次以每件![]() 款童装按进价加价
款童装按进价加价![]() 元进行销售,每件
元进行销售,每件![]() 款童装按进价加价
款童装按进价加价![]() 进行销售,全部销售完.
进行销售,全部销售完.
(1)求购进![]() 两款童装各多少件?
两款童装各多少件?
(2)春节期间该商场按上次进价又购进与上一次一样数量的![]() 两款童装,并展开了降价促销活动,在促销期间,该商场将每件
两款童装,并展开了降价促销活动,在促销期间,该商场将每件![]() 款童装按进价提高
款童装按进价提高![]() 进行销售,每件
进行销售,每件![]() 款童装按上次售价降低
款童装按上次售价降低![]() 销售.结果全部销售完后销售利润比上次利润少了
销售.结果全部销售完后销售利润比上次利润少了![]() 元,求
元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA为⊙O的切线,A为切点,直线PO交⊙O于点E,F过点A作PO的垂线AB垂足为D,交⊙O于点B,延长BO与⊙O交与点C,连接AC,BF.
(1)求证:PB与⊙O相切;
(2)是探究线段EF,OD,OP之间的数量关系,并加以证明;
(3)若tan∠F= ![]() ,求cos∠ACB的值.
,求cos∠ACB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,正方形ABCD的边长为6,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() ABCD中,F是AD的中点,延长BC到点E,使CE=
ABCD中,F是AD的中点,延长BC到点E,使CE=![]() BC,连结DE,CF。
BC,连结DE,CF。

(1)求证:四边形CEDF是平行四边形;
(2)若AB=4,AD=6,∠B=60°,求DE的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.试解答下列问题:
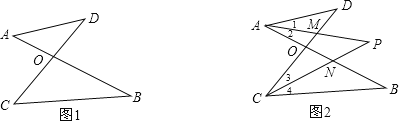
(1)在图1中,写出∠A,∠B,∠C,∠D之间的关系为
(2)如图2,在图1的结论下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.
①仔细观察,在图2中“8字形”的个数:______个;
②若![]() ,
,![]() ,试求∠P的度数;
,试求∠P的度数;
③∠B和∠D为任意角时,其他条件不变,试直接写出∠P与∠B,∠D之间的数量关系,不需要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC的垂直平分线分别交AC、BC于E,D两点,EC=4,△ABC的周长为23,则△ABD的周长为( ) 
A.13
B.15
C.17
D.19
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的对角线相交于点O,且点O是BD的中点,若AB=AD=5,BD=8,∠ABD=∠CDB,则四边形ABCD的面积为( )

A.40B.24C.20D.15
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com