
【题目】已知如图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.试解答下列问题:
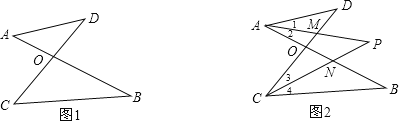
(1)在图1中,写出∠A,∠B,∠C,∠D之间的关系为
(2)如图2,在图1的结论下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.
①仔细观察,在图2中“8字形”的个数:______个;
②若![]() ,
,![]() ,试求∠P的度数;
,试求∠P的度数;
③∠B和∠D为任意角时,其他条件不变,试直接写出∠P与∠B,∠D之间的数量关系,不需要说明理由.
【答案】(1)∠A+∠D=∠B+∠C;(2)①6;②![]() ;③
;③![]() .
.
【解析】
(1)利用三角形外角定理和对顶角相等,即可得出∠A+∠D=∠B+∠C;
(2)①通过分析图1中“8字形”的结构,可通过任意两条不相交的直线和其内部的直线结构来判断图2中“8字形”的数量;
②利用第(1)的结论可知∠1+∠D=∠3+∠P,∠2+∠P=∠4+∠B,再根据平分线的性质,将上式分别相减,即可得到∠P的度数;
③根据第②题的结论即可解答.
解:(1)根据三角形外角定理可得:
∠A+∠D=∠DOB
∠B+∠C =∠AOC
在根据对顶角相等,得
∠DOB=∠AOC
∴∠A+∠D=∠B+∠C;
(2)①6;
②∵∠DAB和∠BCD的平分线AP和CP相交于点P,
∴∠1=∠2,∠3=∠4,
∵∠1+∠D=∠3+∠P,∠2+∠P=∠4+∠B,
∴∠D∠P=∠P∠B,
即∠P=![]() (∠D+∠B),
(∠D+∠B),
∵∠D=40,∠B=36
∴∠P=![]() (40+36)=38;
(40+36)=38;
③由第②题可得
∠P=![]() (∠B+∠D).
(∠B+∠D).


科目:初中数学 来源: 题型:
【题目】本学期我们学习了一元一次方程的解法,下面是小亮同学的解题过程:
解方程:![]()
解:方程两边同时乘以15,去分母,得3(20x﹣3)﹣5(10x+4)=15……①
去括号,得60x﹣9﹣50x+20=15……②
移项,得60x﹣50x=15+9﹣20……③
合并同类项,得10x=4……④
系数化1,得x=0.4……⑤
所以x=0.4原方程的解
(1)上述小亮的解题过程从第 (填序号)步开始出现错误,错误的原因是 .
(2)请写出此题正确的解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y= ![]() 的图象与二次函数y=﹣x2+bx+c的图象在第一象限内相交A、B两点,A、B两点的纵坐标分别为1,3,且AB=2
的图象与二次函数y=﹣x2+bx+c的图象在第一象限内相交A、B两点,A、B两点的纵坐标分别为1,3,且AB=2 ![]()

(1)求反比例函数的解析式;
(2)求二次函数的解析式;
(3)如果M为x轴上一点,N为y轴上一点,以点A,B,M,N为顶点的四边形是平行四边形,试求直线MN的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列例题的解题过程,并完成相关问题
例:如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8 cm,AD=12cm,BC=18cm,点P从点A出发,以1cm/s的速度向点D运动;点Q从点C同时出发,以2cm/s的速度向点B运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.从运动开始,使PQ∥CD和PQ=CD,分别经过多长时间?为什么?
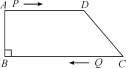
解:①设经过ts时,PQ∥CD且PQ=CD,此时四边形PQCD为平行四边形.
∵PD=(12-t)cm,CQ=2t cm,
∴12-t=2t.∴t=4.
∴当t=4时,PQ∥CD,且PQ=CD.
②设经过ts时,PQ=CD,分别过点P,D作BC边的垂线PE,DF,垂足分别为E,F.
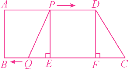
当CF=EQ时,四边形PQCD为梯形(腰相等)或者平行四边形.
∵∠B=∠A=∠DFB=90°,
∴四边形ABFD是矩形.∴AD=BF.
∵AD=12 cm,BC=18 cm,
∴CF=BC-BF=6 cm.
当四边形PQCD为梯形(腰相等)时,
PD+2(BC-AD)=CQ,
∴(12-t)+12=2t.∴t=8.
∴当t=8时,PQ=CD.
当四边形PQCD为平行四边形时,由①知当t=4时,PQ=CD.
综上,当t=4时,PQ∥CD;当t=4或t=8时,PQ=CD.
问题1:在整个运动过程中是否存在t值,使得四边形PQCD是菱形?若存在,请求出t值;若不存在,请说明理由.
问题2:从运动开始,当t取何值时,四边形PQBA是矩形?
问题3:在整个运动过程中是否存在t值,使得四边形PQBA是正方形?若存在,请求出t值;若不存在,请说明理由.
问题4:是否存在t,使得△DQC是等腰三角形?若存在,请求出t值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(6分)△ABC与△A′B′C′在平面直角坐标系中的位置如图.

(1)分别写出下列各点的坐标:A′ ; B′ ;C′ ;
(2)说明△A′B′C′由△ABC经过怎样的平移得到? .
(3)若点P(a,b)是△ABC内部一点,则平移后△A′B′C′内的对应点P′的坐标为 ;
(4)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
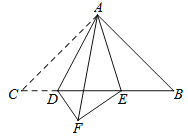
【题目】已知:如图,△ABC 中,∠CAB=90°,AC=AB,点 D、E 是 BC 上的两点,且∠DAE=45°,△ADC 与△ADF 关于直线AD 对称.
(1)求证:△AEF≌△AEB;
(2)求∠DFE 的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知FG⊥AB,CD⊥AB,垂足分别为G,D,∠1=∠2,
求证:∠CED+∠ACB=180°,
请你将小明的证明过程补充完整.
证明:∵FG⊥AB,CD⊥AB,垂足分别为G,D(已知)
∴∠FGB=∠CDB=90°( ).
∴GF∥CD( )
∵GF∥CD(已证)
∴∠2=∠BCD( )
又∵∠1=∠2(已知)
∴∠1=∠BCD( )
∴ ( )
∴∠CED+∠ACB=180°( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料;
课堂上,老师设计了一个活动:将一个4×4的正方形网格沿着网格线划分成两部分(分别用阴影和空白表示),使得这两部分图形是全等的,请同学们尝试给出划分的方法.约定:如果两位同学的划分结果经过旋转、翻折后能够重合,那么就认为他们的划分方法相同.
小方、小易和小红分别对网格进行了划分,结果如图①、图②、图③所示.
小方说:“我们三个人的划分方法都是正确的,但是将小红的整个图形(图③)逆时针旋转90![]() 后得到的划分方法与我的划分方法(图①)是一样的,应该认为是同一种方法,而小易的划分方法与我的不同,”
后得到的划分方法与我的划分方法(图①)是一样的,应该认为是同一种方法,而小易的划分方法与我的不同,”
老师说:“小方说得对.”

完成下列问题:
(1)图④的划分方法是否正确?
(2)判断图⑤的划分方法与图②小易的划分方法是否相同,并说明你的理由.
(3)请你再想出一种与已有方法不同的划分方法,使之满足上述条件,并在图⑥中画出来.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com