
【题目】如图,反比例函数y= ![]() 的图象与二次函数y=﹣x2+bx+c的图象在第一象限内相交A、B两点,A、B两点的纵坐标分别为1,3,且AB=2
的图象与二次函数y=﹣x2+bx+c的图象在第一象限内相交A、B两点,A、B两点的纵坐标分别为1,3,且AB=2 ![]()

(1)求反比例函数的解析式;
(2)求二次函数的解析式;
(3)如果M为x轴上一点,N为y轴上一点,以点A,B,M,N为顶点的四边形是平行四边形,试求直线MN的函数表达式.
【答案】
(1)解:∵A、B两点都在反比例函数y= ![]() 的图象上,两点的纵坐标分别为1,3,
的图象上,两点的纵坐标分别为1,3,
故可设A(x1 , 1)B(x2 , 3),分别代入反比例函数的解析式为k=x1 , k=3x2 ,
解得x1=3x2 ,
由AB=2 ![]() ,
,
可得(x1﹣x2)2+(1﹣3)2=(2 ![]() )2 , x2=±2,
)2 , x2=±2,
因为函数图象在第一象限,
故x2=2,k=3x2=6,
∴该反比例函数的解析式为:
y= ![]()
(2)由(1)可知,A(6,1),B(2,3),代入二次函数的解析式,
得 ![]() ,
,
解得 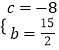 ,
,
故此二次函数的解析式为:y=﹣x2+ ![]() x﹣8
x﹣8
(3)解:设M(x,0),N(0,y),过A、B两点的直线解析式为y=kx+b,
把A、B两点坐标代入得 ![]() ,
,
解得k=﹣ ![]() .
.
则设经过M、N两点的直线解析式为y=﹣ ![]() x+b,
x+b,
把M(x,0),N(0,y)代入得y=b,x=2b,
∵MN=AB,即x2+y2=(2 ![]() )2 , 即b2=4,b=±2,
)2 , 即b2=4,b=±2,
故过M,N两点的直线解析式为:y=﹣ ![]() x+2或y=﹣
x+2或y=﹣ ![]() x﹣2
x﹣2
【解析】本题考查的是一次函数,反比例函数及二次函数图象上点的坐标特点,涉及面较广,但难度适中.
小题1 设出A、B两点的坐标,根据两点都在反比例函数的图象上,可找出两坐标之间的关系,由AB两点之间的距离可求出K的值,从而求出其解析式;
小题2 根据小题1中所求A,B两点的坐标,分别代入二次函数的解析式即可求出b、c的值,从而求出二次函数的解析式;
小题3 设出M,N两点的坐标,由A,B两点的坐标可求出过A,B两点直线的解析式,根据其解析式可设出过M,N两点的直线解析式,找出两点坐标与的关系,再根据平行四边形的性质即可求出未知数的值从而求出其解析式.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,AB=AC,BC= ![]() +1,点M,N分别是边BC,AB上的动点,沿MN所在的直线折叠∠B,使点B的对应点B′始终落在边AC上,若△MB′C为直角三角形,则BM的长为 .
+1,点M,N分别是边BC,AB上的动点,沿MN所在的直线折叠∠B,使点B的对应点B′始终落在边AC上,若△MB′C为直角三角形,则BM的长为 . 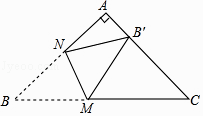
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有A、B两组卡片共5张,A组的三张分别写有数字2,4,6,B组的两张分别写有3,5.它们除了数字外没有任何区别,
(1)随机从A组抽取一张,求抽到数字为2的概率;
(2)随机地分别从A组、B组各抽取一张,请你用列表或画树状图的方法表示所有等可能的结果.现制定这样一个游戏规则:若选出的两数之积为3的倍数,则甲获胜;否则乙获胜.请问这样的游戏规则对甲乙双方公平吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年1月重庆湖童时装周在重庆渝北举行了八场走秀,云集了八大国内外潮童品牌,不仅为大家带来了一场品牌走秀盛会,更让人们将目光转移到了![]() 后、
后、![]() 后童模群体身上,开启服装新秀湖流.某大型商场抓住这次商机购进
后童模群体身上,开启服装新秀湖流.某大型商场抓住这次商机购进![]() 两款新童装进行试销售,该商场用
两款新童装进行试销售,该商场用![]() 元购买
元购买![]() 款童装,用
款童装,用![]() 元购买
元购买![]() 款童装,且每件
款童装,且每件![]() 款童装进价与每件
款童装进价与每件![]() 款童装进价相同,购买
款童装进价相同,购买![]() 款童装的数量比
款童装的数量比![]() 款童装的数量少
款童装的数量少![]() 件,若该商场本次以每件
件,若该商场本次以每件![]() 款童装按进价加价
款童装按进价加价![]() 元进行销售,每件
元进行销售,每件![]() 款童装按进价加价
款童装按进价加价![]() 进行销售,全部销售完.
进行销售,全部销售完.
(1)求购进![]() 两款童装各多少件?
两款童装各多少件?
(2)春节期间该商场按上次进价又购进与上一次一样数量的![]() 两款童装,并展开了降价促销活动,在促销期间,该商场将每件
两款童装,并展开了降价促销活动,在促销期间,该商场将每件![]() 款童装按进价提高
款童装按进价提高![]() 进行销售,每件
进行销售,每件![]() 款童装按上次售价降低
款童装按上次售价降低![]() 销售.结果全部销售完后销售利润比上次利润少了
销售.结果全部销售完后销售利润比上次利润少了![]() 元,求
元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4.分别以AB,AC,BC为边在AB的同侧作正方形ABEF,ACPQ,BCMN,四块阴影部分的面积分别为S1,S2,S3,S4,则S1+S2+S3+S4等于____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA为⊙O的切线,A为切点,直线PO交⊙O于点E,F过点A作PO的垂线AB垂足为D,交⊙O于点B,延长BO与⊙O交与点C,连接AC,BF.
(1)求证:PB与⊙O相切;
(2)是探究线段EF,OD,OP之间的数量关系,并加以证明;
(3)若tan∠F= ![]() ,求cos∠ACB的值.
,求cos∠ACB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,正方形ABCD的边长为6,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.试解答下列问题:
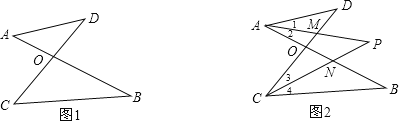
(1)在图1中,写出∠A,∠B,∠C,∠D之间的关系为
(2)如图2,在图1的结论下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.
①仔细观察,在图2中“8字形”的个数:______个;
②若![]() ,
,![]() ,试求∠P的度数;
,试求∠P的度数;
③∠B和∠D为任意角时,其他条件不变,试直接写出∠P与∠B,∠D之间的数量关系,不需要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆经营长途运输的货车在高速公路的A处加满油后,以每小时80千米的速度匀速行驶,前往B地,如表记录的是货车一次加满油后油箱内余油量y(升)与行驶时间x(时)之间的关系:
行驶时间x/时 | 0 | 1 | 2 | 2.5 |
余油量y/升 | 100 | 80 | 60 | 50 |
则y与x的函数关系式为_____,自变量x的取值范围为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com