
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4.分别以AB,AC,BC为边在AB的同侧作正方形ABEF,ACPQ,BCMN,四块阴影部分的面积分别为S1,S2,S3,S4,则S1+S2+S3+S4等于____.

【答案】18
【解析】
过F作AM的垂线交AM于D,连接FP,通过证明△ADF≌△BCA,△DFK≌△CAT,得出S2=S△ABC;证明△FPT≌△EMK,可得出S1+S3=S△AQF=S△ABC;证明△ABC≌△EBN,得出S4=S△ABC,进而即可求解.
解:过F作AM的垂线交AM于D,连接FP,则
∠FDA=∠DAQ=∠Q=90°,∴四边形ADFQ为矩形,∴∠PFD=90°,∴∠FPC=90°,
∴点F,P,Q在同一直线上.
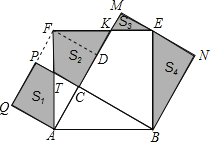
∵四边形ABEF为正方形,
∴AB=AF,∠FAB=90°=∠FAD+∠CAB,
又∠ACB=90°,∴∠CAB+∠ABC=90°,
∴∠FAD=∠ABC,
又∠ACB=∠ADF=90°
∴△ADF≌△BCA(AAS)①,
∴DF=AC,同理可得△DFK≌△CAT,
∴S2=S△ADF=S△ABC.
由△DFK≌△CAT,∴FK=AT,∠DKF=∠CTA,
∴KE=FT,∠EKM=∠FTP,又∠M=∠FPT=90°,
∴△FPT≌△EMK(AAS),
∴S3=S△FPT,
又四边形ADFQ为矩形,∴S△AQF=S△ADF =S△ACB,
∴S1+S3=S△AQF=S△ABC.
同①可证明△ABC≌△EBN,
∴S4=S△ABC,
∴S1+S2+S3+S4=(S1+S3)+S2+S4=S△ABC+S△ABC+S△ABC=6+6+6=18,
故答案为:18.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】重庆实验外国语学校运动会期间,小明和小欢两人打算匀速从教室跑到600米外的操场参加入场式,出发时小明发现鞋带松了,停下来系鞋带,小欢继续跑往操场,小明系好鞋带后立即沿同一路线开始追赶小欢.小明在途中追上小欢后继续前行,小明到达操场时入场式还没有开始,于是小明站在操场等待,小欢继续前往操场.设小明和小欢两人相距![]() (米),小欢行走的时间为
(米),小欢行走的时间为![]() (分钟),
(分钟),![]() 关于
关于![]() 的函数图像如图所示,则在整个运动过程中,小明和小欢第一次相距
的函数图像如图所示,则在整个运动过程中,小明和小欢第一次相距![]() 米后,再过_____分钟两人再次相距
米后,再过_____分钟两人再次相距![]() 米.
米.
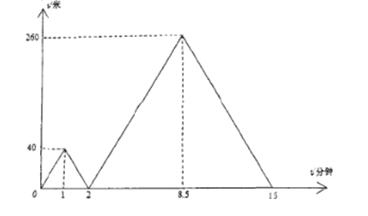
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,点![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标是
的坐标是![]() ,点
,点![]() 和点
和点![]() 关于原点对称,点
关于原点对称,点![]() 是直线
是直线![]() 位于
位于![]() 轴右侧部分图象上一点,连接
轴右侧部分图象上一点,连接![]() ,已知
,已知![]() .
.
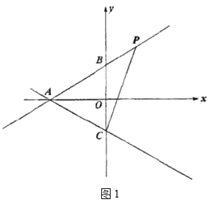
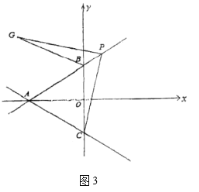
(1)求直线![]() 的解析式;
的解析式;
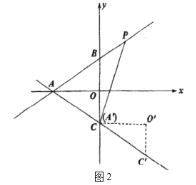
(2)如图2,![]() 沿着直线
沿着直线![]() 平移得
平移得![]() ,平移后的点
,平移后的点![]() 与点
与点![]() 重合.点
重合.点![]() 为直线
为直线![]() 上的一动点,当
上的一动点,当![]() 的值最小时,请求出
的值最小时,请求出![]() 的最小值及此时点
的最小值及此时点![]() 的坐标;
的坐标;
(3)如图3,将![]() 沿直线
沿直线![]() 是翻折得
是翻折得![]() 点
点![]() 为平面内任意一动点,在直线
为平面内任意一动点,在直线![]() 上是否存在一点
上是否存在一点![]() ,使得以点
,使得以点![]() 为顶点的四边形是矩形;若存在,请直接写出点
为顶点的四边形是矩形;若存在,请直接写出点![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y= ![]() 的图象与二次函数y=﹣x2+bx+c的图象在第一象限内相交A、B两点,A、B两点的纵坐标分别为1,3,且AB=2
的图象与二次函数y=﹣x2+bx+c的图象在第一象限内相交A、B两点,A、B两点的纵坐标分别为1,3,且AB=2 ![]()

(1)求反比例函数的解析式;
(2)求二次函数的解析式;
(3)如果M为x轴上一点,N为y轴上一点,以点A,B,M,N为顶点的四边形是平行四边形,试求直线MN的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如3+2![]() =(1+
=(1+![]() )2,善于思考的小明进行了以下探索:设a+b
)2,善于思考的小明进行了以下探索:设a+b![]() =(m+n
=(m+n![]() )2(其中a,b,m,n均为正整数),则有a+b
)2(其中a,b,m,n均为正整数),则有a+b![]() =m2+2n2+2
=m2+2n2+2![]() mn,∴a=m2+2n2,b=2mn.
mn,∴a=m2+2n2,b=2mn.
这样小明就找到了一种把a+b![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当a,b,m,n均为正整数时,若a+b![]() =(m+n
=(m+n![]() )2,用含m,n的式子分别表示a,b,得a= ,b= ;
)2,用含m,n的式子分别表示a,b,得a= ,b= ;
(2)利用所探索的结论,找一组正整数a,b,m,n填空:4+2 =(1+ )2;(答案不唯一)
(3)若a+4![]() =(m+n
=(m+n![]() )2,且a,m,n均为正整数,求a的值.
)2,且a,m,n均为正整数,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,AC=BC=2,正方形CDEF的顶点D、F分别在AC,BC边上,C,D两点不重合,设CD的长度为x,△ABC与正方形CDEF重叠部分的面积为y,则下列图象中能表示y与x之间的函数关系的是( )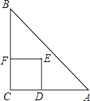
A.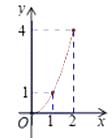
B.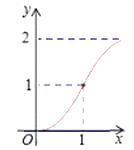
C.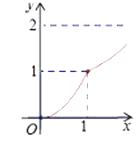
D.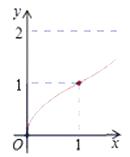
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com