Question

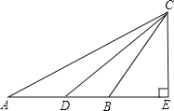
【题目】在△ABC中，∠A=∠ACB，CD是△ABC的角平分线，CE是△ABC的高．

（1）试说明∠CDB=3∠DCB．

（2）若∠DCE=48°，求∠ACB的度数．

Answer 1

【答案】(1)见解析；(2)28°.

【解析】

(1)根据题意设∠A为2x，则∠ACB=2x，∠ACD=x，由三角形的外角定理得出∠CDB=∠A+∠ACD=3x，即可得出结论；

(2)求出∠CDB=42°，由(1)得出∠DCB=14°得出∠ACB=28°即可．

解：(1)证明：由题意设∠A=2x，

∴∠A=∠ACB=2x，

∵CD是∠ACB的角平分线，

∠ACD=∠DCB=x，

∴由三角形的外角定理可知：

∠CDB=∠A+∠ACD=2x+x=3x，

∴∠CDB=3∠DCB．

(2)∵CE是△ABC的高，

∴∠E=90°，

∵∠DCE=48°，

∴∠CDB=∠E-∠DCE=90°- 48°= 42°，

由(1)可知∠CDB=3∠DCB=42°，

∴∠DCB=14°

∴∠ACB=2∠DCB=2×14°=28°．

故答案为：28°.