
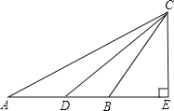
【题目】已知,在平面直角坐标系中,A(m,0)、B(0,n),m、n满足(m-n)2+|m-![]() |=0.C为AB的中点,P是线段AB上一动点,D是x轴正半轴上一点,且PO=PD,DE⊥AB于E.
|=0.C为AB的中点,P是线段AB上一动点,D是x轴正半轴上一点,且PO=PD,DE⊥AB于E.

(1)求∠OAB的度数;
(2)设AB=4,当点P运动时,PE的值是否变化?若变化,说明理由;若不变,请求PE的值;
(3)设AB=4,若∠OPD=45°,求点D的坐标.
【答案】(1)∠OAB=45°.(2)![]()
【解析】
(1)根据非负数的性质即可求得a,b的值,从而得到△AOB是等腰直角三角形,据此即可求得;
(2)根据等腰三角形的性质以及三角形的外角的性质可以得到∠POC=∠DPE,即可证得△POC≌△DPE,则OC=PE,OC的长度根据等腰直角三角形的性质可以求得;
(3)利用等腰三角形的性质,以及外角的性质证得∠POC=∠DPE,即可证得△POC≌△DPE,根据全等三角形的对应边相等,即可求得OD的长,从而求得D的坐标.
解:(1)根据题意得:
 ,
,
解得:m=n=![]() ,
,
∴OA=OB, 又∵∠AOB=90°
∴△AOB为等腰直角三角形,
∴∠OAB=45°.
(2)PE的值不变.理由如下:
∵△AOB为等腰直角三角形,且AC=BC, ∴∠AOC=∠BOC=45°
又∵OC⊥AB于C, ∵PO=PD ∴∠POD=∠PDO
当P在BC上时,
∵∠POD=45°+∠POC,∠PDO=45°+∠DPE,
∴∠POC=∠DPE
在△POC和△DPE中,

∴△POC≌△DPE,∴OC=PE
又![]() ∴PE=2;
∴PE=2;
当P在AC上时,∠POD=45°﹣∠POC,∠PDO=45°﹣∠DPE,
则∠POC=∠DPE.
同理可得PE=2;
(3)∵OP=PD,
∴![]() ,
,
则∠PDA=180°﹣∠PDO=180°﹣67.5°=112.5°,
∵∠POD=∠A+∠APD,
∴∠APD=67.5°﹣45°=22.5°,
∴∠BPO=180°﹣∠OPD﹣∠APD=112.5°,
∴∠PDA=∠BPO
则在△POB和△DPA中,

∴△POB≌△DPA(AAS).
∴PA=OB=![]() ,
,
∴DA=PB=![]()
∴OD=OA﹣DA=![]()
∴ ![]()



科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,∠C=90°,∠A=34°,D,E 分别为 AB,AC 上一点,将△BCD,△ADE 沿 CD,DE 翻折,点 A,B 恰好重合于点 P 处,则∠ACP=_______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某经销商经销的学生用品,他以每件280元的价格购进某种型号的学习机,以每件360元的售价销售时,每月可售出60个,为了扩大销售,该经销商采取降价的方式促销,在销售中发现,如果每个学习机降价1元,那么每月就可以多售出5个.
![]() 降价前销售这种学习机每月的利润是多少元?
降价前销售这种学习机每月的利润是多少元?
![]() 经销商销售这种学习机每月的利润要达到7200元,且尽可能让利于顾客,求每个学习机应降价多少元?
经销商销售这种学习机每月的利润要达到7200元,且尽可能让利于顾客,求每个学习机应降价多少元?
![]() 在
在![]() 的销售中,销量可好,经销商又开始涨价,涨价后每月销售这种学习机的利润能达到10580元吗?若能,请求出涨多少元;若不能,请说明理由.
的销售中,销量可好,经销商又开始涨价,涨价后每月销售这种学习机的利润能达到10580元吗?若能,请求出涨多少元;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是本地区一种产品30天的销售图象,图1是产品日销售量y(单位:件)与时间t(单位:天)的函数关系,图2是一件产品的销售利润z(单位:元)与时间t(单位:天)的函数关系,已知日销售利润=日销售量×一件产品的销售利润,下列结论错误的是( )

A. 第24天的销售量为200件 B. 第10天销售一件产品的利润是15元
C. 第12天与第30天这两天的日销售利润相等 D. 第30天的日销售利润是750元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是橘子的销售额随橘子卖出质量的变化表:
质量/千克 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | … |
销售额/元 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | … |
(1)这个表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当橘子卖出5千克时,销售额是_______元.
(3)如果用![]() 表示橘子卖出的质量,
表示橘子卖出的质量,![]() 表示销售额,按表中给出的关系,
表示销售额,按表中给出的关系,![]() 与
与![]() 之间的关系式为______.
之间的关系式为______.
(4)当橘子的销售额是100元时,共卖出多少千克橘子?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图所示,直线MN∥GH,另一直线交GH于A,交MN于B,且∠MBA=80°,点C为直线GH上一动点,点D为直线MN上一动点,且∠GCD=50°.

(1)如图1,当点C在点A右边且点D在点B左边时,∠DBA的平分线交∠DCA的平分线于点P,求∠BPC的度数;
(2)如图2,当点C在点A右边且点D在点B右边时,∠DBA的平分线交∠DCA的平分线于点P,求∠BPC的度数;
(3)当点C在点A左边且点D在点B左边时,∠DBA的平分线交∠DCA的平分线所在直线交于点P,请直接写出∠BPC的度数,不说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,在△ABC中,∠ACB=900,AC=12,BC=5,AM=AC,BN=BC,求MN的长.

(2)如图,在△ABC中,∠ACB=900,AM=AC,BN=BC
当∠A=300时,求∠MCN的度数。
当∠A的度数变化时,∠MCN的度数是否变化,如有变化,请说明理由;如不变,求∠MCN的度数.

(3)如图,在△ABC中,∠ACB=90,AC=BC,点M、N在边AB上,且∠MCN=450,试猜想线段AN、BM、MN之间的数学关系,直接写出你的结论(不要求证明).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A是反比例函数![]() 的图象在第一象限上的动点,连结AO并延长交另一分支于点B,以AB为边作等边
的图象在第一象限上的动点,连结AO并延长交另一分支于点B,以AB为边作等边![]() 使点C落在第二象限,且边BC交x轴于点D,若
使点C落在第二象限,且边BC交x轴于点D,若![]() 与
与![]() 的面积之比为1:2,则点C的坐标为
的面积之比为1:2,则点C的坐标为![]()
![]()

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠A=∠ACB,CD是△ABC的角平分线,CE是△ABC的高.
(1)试说明∠CDB=3∠DCB.
(2)若∠DCE=48°,求∠ACB的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com