
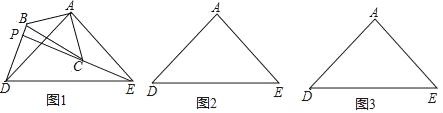
【题目】如图所示,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,EC的延长线交BD于点P.
(1)把△ABC绕点A旋转到图1,BD,CE的关系是 (选填“相等”或“不相等”);简要说明理由;
(2)若AB=3,AD=5,把△ABC绕点A旋转,当∠EAC=90°时,在图2中作出旋转后的图形,PD= ,简要说明计算过程;
(3)在(2)的条件下写出旋转过程中线段PD的最小值为 ,最大值为 .
【答案】(1)BD,CE的关系是相等;(2)![]() 或
或![]() ;(3)1,7
;(3)1,7
【解析】分析:(1)依据△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,即可BA=CA,∠BAD=∠CAE,DA=EA,进而得到△ABD≌△ACE,可得出BD=CE;
(2)分两种情况:依据∠PDA=∠AEC,∠PCD=∠ACE,可得△PCD∽△ACE,即可得到![]() =
=![]() ,进而得到PD=
,进而得到PD=![]() ;依据∠ABD=∠PBE,∠BAD=∠BPE=90°,可得△BAD∽△BPE,即可得到
;依据∠ABD=∠PBE,∠BAD=∠BPE=90°,可得△BAD∽△BPE,即可得到![]() ,进而得出PB=
,进而得出PB=![]() ,PD=BD+PB=
,PD=BD+PB=![]() ;
;
(3)以A为圆心,AC长为半径画圆,当CE在⊙A下方与⊙A相切时,PD的值最小;当CE在在⊙A右上方与⊙A相切时,PD的值最大.在Rt△PED中,PD=DEsin∠PED,因此锐角∠PED的大小直接决定了PD的大小.分两种情况进行讨论,即可得到旋转过程中线段PD的最小值以及最大值.
详解:(1)BD,CE的关系是相等.
理由:∵△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,
∴BA=CA,∠BAD=∠CAE,DA=EA,
∴△ABD≌△ACE,
∴BD=CE;
故答案为:相等.
(2)作出旋转后的图形,若点C在AD上,如图2所示:
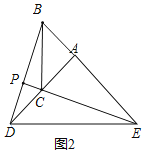
∵∠EAC=90°,
∴CE=![]() ,
,
∵∠PDA=∠AEC,∠PCD=∠ACE,
∴△PCD∽△ACE,
∴![]() ,
,
∴PD=![]() ;
;
若点B在AE上,如图2所示:
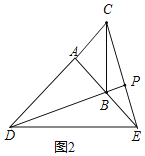
∵∠BAD=90°,
∴Rt△ABD中,BD=![]() ,BE=AE﹣AB=2,
,BE=AE﹣AB=2,
∵∠ABD=∠PBE,∠BAD=∠BPE=90°,
∴△BAD∽△BPE,
∴![]() ,即
,即![]() ,
,
解得PB=![]() ,
,
∴PD=BD+PB=![]() +
+![]() =
=![]() ,
,
故答案为:![]() 或
或![]() ;
;
(3)如图3所示,以A为圆心,AC长为半径画圆,当CE在⊙A下方与⊙A相切时,PD的值最小;当CE在在⊙A右上方与⊙A相切时,PD的值最大.
如图3所示,分两种情况讨论:
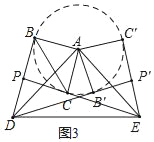
在Rt△PED中,PD=DEsin∠PED,因此锐角∠PED的大小直接决定了PD的大小.
①当小三角形旋转到图中△ACB的位置时,
在Rt△ACE中,CE=![]() =4,
=4,
在Rt△DAE中,DE=![]() ,
,
∵四边形ACPB是正方形,
∴PC=AB=3,
∴PE=3+4=7,
在Rt△PDE中,PD=![]() ,
,
即旋转过程中线段PD的最小值为1;
②当小三角形旋转到图中△AB'C'时,可得DP'为最大值,
此时,DP'=4+3=7,
即旋转过程中线段PD的最大值为7.
故答案为:1,7.


科目:初中数学 来源: 题型:
【题目】下表是小华同学一个学期数学成绩的记录.根据表格提供的信息,回答下列的问题:
考试类别 | 平时考试 | 期中考试 | 期末考试 | |||
第一单元 | 第二单元 | 第三单元 | 第四单元 | |||
成绩(分) | 85 | 78 | 90 | 91 | 90 | 94 |
(1)小明6次成绩的众数是 ,中位数是 ;
(2)求该同学这个同学这一学期平时成绩的平均数;
(3)总评成绩权重规定如下:平时成绩占20%,期中成绩占30%,期末成绩占50%,请计算出小华同学这一个学期的总评成绩是多少分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】徐州至北京的高铁里程约为700km,甲、乙两人从徐州出发,分别乘坐“徐州号”高铁A与“复兴号”高铁B前往北京.已知A车的平均速度比B车的平均速度慢80km/h,A车的行驶时间比B车的行驶时间多40%,两车的行驶时间分别为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)已知△ABC是等边三角形,点D是直线BC上一点,以AD为一边在AD的右侧作等边△ADE.
(1)如图①,点D在线段BC上移动时,直接写出∠BAD和∠CAE的大小关系;
(2)如图②,点D在线段BC的延长线上移动时,猜想∠DCE的大小是否发生变化.若不变请求出其大小;若变化,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某闭合电路中,其两端电压恒定,电流I(A)与电阻R(Ω)图象如图所示,回答问题: 
(1)写出电流I与电阻R之间的函数解析式.
(2)如果一个用电器的电阻为5Ω,其允许通过的最大电流是1A,那么这个用电器接在这个闭合电路中,会不会烧毁?说明理由.
(3)若允许的电流不超过4A时,那么电阻R的取值应该控制在什么范围?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过点A(2,0)的两条直线![]() ,
,![]() 分别交
分别交![]() 轴于B,C,其中点B在原点上方,点C在原点下方,已知AB=
轴于B,C,其中点B在原点上方,点C在原点下方,已知AB=![]() .
.

(1)求点B的坐标;
(2)若△ABC的面积为4,求![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王沿街匀速行走,发现每隔6分钟从背后驶过一辆18路公交车,每隔3分钟从迎面驶来一辆18路公交车.假设每辆18路公交车行驶速度相同,而且18路公交车总站每隔固定时间发一辆车,那么发车间隔的时间是( )
A. 3分钟 B. 4分钟 C. 5分钟 D. 6分钟
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com