
����Ŀ�����������������εı߳�����20cm����ֱ�����Ҫ�����һ�ּ�ƴ�����������߱�ʾ�����Ʒ������Ѽ�ƴ�߶��ôֺ�ʵ�ߣ���ͼ�б�ע����Ҫ�ķ��ź����ݣ�������Ҫ˵���� 
��1����ͼ1�е�������ֽƬ��ƴ��һ�������������ε�ֱ������ģ�ͣ�ʹ���ı������ԭ�����������ȣ�
��2����ͼ2�е���������ֽƬ��ƴ��һ���������������ε�ֱ������ģ�ͣ�ʹ���ı������ԭ�������ε������ȣ�
��3����ͼ3�е��������ֽƬ��ƴ��һ��������������ε�ֱ������ģ�ͣ�ʹ���ı������ԭ������ε������ȣ�
���𰸡�
��1���⣺��ͼ1���غ��������Ѽ��µ��ĸ�С������ƴ��һ�������Σ����������۵�����

��2���⣺��ͼ2���غ��������Ѽ��µ�������ƴ��һ���������Σ����������۵����ɣ�

��3���⣺��ͼ3���غ��������Ѽ��µ��岿��ƴ��һ��������Σ����������۵����ɣ�

����������1�����������ĸ����Ϸֱ����һ���߳�Ϊ5��С�����Σ�ƴ��һ����������Ϊֱ�������ĵ��漴�ɣ���2�����������ε�ÿһ�����ҳ������������5�ĵ㣬Ȼ�����ߵĴ��ߣ����º�ƴ��һ���������Σ���Ϊֱ��������һ�����漴�ɣ���3����������ε�ÿһ�����ҳ������������5�ĵ㣬Ȼ�����ߵĴ��ߣ����º�ƴ��һ��������Σ���Ϊֱ��������һ�����漴�ɣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ɫ���У���̼�������ѳ�Ϊ�������Ĺ�ʶ��ij���ξ���������һ���������г�ͣ������6��00��18��00������ڴ˽������г���Ҳ�ɽ��ڸ�ͣ�������õ����г����ڴ˵أ��ֻ�ͬѧͳ����������ͣ������ʱ�εĽ衢�����г������Լ�ͣ��������ʱ�̵����г���������Ϊ�����������������x=1ʱ��yֵ��ʾ7��00ʱ�Ĵ�����x=2ʱ��yֵ��ʾ8��00ʱ�Ĵ������������ƣ������ִ���y��������x��xΪ������������ͼ��ʾ��һ�����κ�����ϵ�� 
ʱ�� | x | ������ | �賵�� | ����y |
6��00��7��00 | 1 | 45 | 5 | 100 |
7��00��8��00 | 2 | 43 | 11 | n |
�� | �� | �� | �� | �� |
��������ͼ����Ϣ������������⣺
��1��m= �� ����m��ʵ�����壺��
��2��������ʱ�̵����г�����y��x֮������Ķ��κ�����ϵʽ��
��3����֪9��00��10��O0���ʱ�εĻ������Ƚ賵����3����4�����ʱ�εĽ賵����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90�㣬���ۡ�C��ʹ��C����б��AB��ijһ��D�����ۺ�ΪEF����E��F�ֱ��ڱ�AC��BC�ϣ��� 
��1������C��E��FΪ���������������A��B��CΪ��������������ƣ� �ٵ�AC=BC=2ʱ��AD�ij�Ϊ��
�ڵ�AC=3��BC=4ʱ��AD�ij�Ϊ��
��2������D��AB���е�ʱ����CEF���CBA��������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ���ı���ABCD�У�AB��BC=3��2����DAB=60�㣬E��AB�ϣ���AE��EB=1��2��F��BC���е㣬��D�ֱ���DP��AF��P��DQ��CE��Q����DP��DQ���ڣ� �� 
A.3��4
B.![]() ��2
��2 ![]()
C.![]() ��2
��2 ![]()
D.2 ![]() ��
�� ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ�˽⡰�γ�ѡ�ޡ���������Ա����μӡ��������͡������Ƽ�������������ѧ˼ά�������Ķ�д�������ĸ�ѡ����Ŀ��ѧ����ÿ���ޱ�һ�Σ����г������飬�����Ǹ����ռ������ݻ��ƵIJ�������ͳ��ͼ�� 
�����ͼ���ṩ����Ϣ�������������⣺
��1���˴ι���������ѧ��������ͳ��ͼ�С��������͡����ֵ�Բ�Ľ����ȣ�
��2������������ͳ��ͼ����������
��3���ָ�У����800��ѧ�������μ����ĸ�ѡ����Ŀ��������������ж�����ѧ��ѡ�ޡ��Ƽ���������Ŀ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������x��һԪ���η���x2+��2k+1��x+k2+1=0����������ʵ��x1 �� x2 �� ��ʵ��k��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�߶�d���߶�a��b��c�ĵ��ı��������a=2cm��b=4cm��c=5cm����d���ڣ�������.
A.1cm
B.10cm
C.2.5cm
D.1.6cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У�EΪCD��һ�㣬����AE��BD �� ��AE��BD���ڵ�F �� DE��EC=2��3����S��DEF��S��ABF=�������� 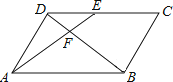
A.2��3
B.4��9
C.2��5
D.4��25
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס���������Լ��ĩ�ǻ���ɽ���ס������˾����ĸ߶�y���ף����ɽʱ��x���֣�֮��ĺ���ͼ����ͼ��ʾ������ͼ�����ṩ����Ϣ����������⣺
(1)��ɽ�������ٶ���ÿ������ ���ף�����A��ʱ�����ĸ߶�bΪ�� ���ף�
(2)�������ٺ��ҵĵ�ɽ�����ٶ��Ǽ�ɽ�����ٶȵ�3����������ҵ�ɽȫ���У������ĸ߶�y���ף����ɽʱ��x���֣�֮��ĺ�����ϵʽ��
(3)��ɽ�ʱ��ʱ���ס������˾����ĸ߶Ȳ�Ϊ70�ף�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com