
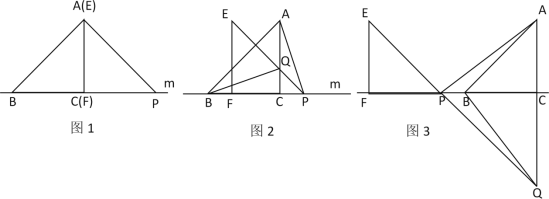
����Ŀ����1�������龳����ͼ1����ABC�ı�BC��ֱ��m�ϣ�AC��BC����AC=BC����EFP�ı�FPҲ��ֱ��m�ϣ���EF���AC�غϣ���EF=FP��
��ͼ1�У�AB��AP��������ϵ��_______��AB��AP��λ�ù�ϵ��_______
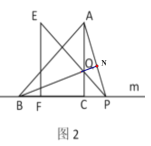
��2���������֣�����EFP��ֱ��m����ƽ�Ƶ�ͼ2��λ��ʱ��EP��AC�ڵ�Q������AP��BQ�����벢֤��BQ��AP��������ϵ��λ�ù�ϵ
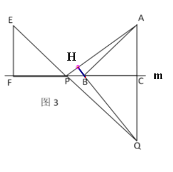
��3��������֤������EFP��ֱ��m����ƽ�Ƶ�ͼ3��λ��ʱ��EP���ӳ��߽�AC���ӳ����ڵ�Q������AP��BQ����2���еĽ��ۻ�������Ϊʲô��
���𰸡���1����ȣ���ֱ��2����ȣ���ֱ,֤���ԣ�3������,֤����
��������
��1����˵����ABC���EFP��ȫ�ȵĵ���ֱ�������Σ�Ȼ����ݵ���ֱ�����ǵ����ʿɵ� ��BAC=��CAP=45�㣬��AB=AP���֡�BAP=90�㣬��AP��AB��
��2���ӳ�BQ��AP��H�㣬˵����QPCΪ����ֱ�������Σ�����QC=PC��Ȼ���ж���ACP�ա�BCQ����AP=BQ����BQC=��APC����������ֱ�������ε�����˵����PNB=90�㼴�ɣ�
��3������ͬ��2����֤BQ��AP�������������ϵΪ��ȣ�λ�ù�ϵΪ��ֱ��
�⣺��ͼ1��������ã�AC��BC��AC=BC��EF=AC��EF=FP��
���ABC���EFP��ȫ�ȵĵ���ֱ��������
���BAC=��CAP=45��
��AB=AP
�֡ߡ�BAP=��BAC����CAP= 90��
��AP��AB
�ʴ�ΪAB=AP��AP��AB��
��2��֤������ͼ���ӳ�BQ��AP��H�㣬
�ߡ�EPF=45
���CPQ=45��
��AC��BC.
���COP=��CPQ.
��CQ=CP������QPCΪ����ֱ��������
��Rt��BCQ��Rt��ACP��
BC=AC����BCQ=��ACP�� CQ=CP��
��Rt��BCQ��Rt��ACP��SAS��
��BQ=AP����BQC=��APC��
��Rt��BCQ����BQC+��PBN=90��
���APC+��PBN=90��
���PNB=90��
��QB��AP
��3������,�������£�
��ͼ3���ߡ�EPF=45
���CPQ=45��
��AC��BC.
���COP=��CPQ.
��CQ=CP������QPCΪ����ֱ��������
��Rt��BCQ��Rt��ACP��
BC=AC����BCQ=��ACP�� CQ=CP��
��Rt��BCQ��Rt��ACP��SAS��
��BQ=AP����BQC=��APC��
��Rt��BCQ����BQC+��CBQ=90��
�ߡ�PBH=��CBQ
���APC+��PBH=90��
���PHB=180��-����APC+��PBH��=90��
��QB��AP



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����OΪԭ�㣬A. BΪ���������㣬AB=15����OA:OB=2.
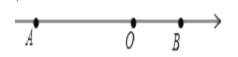
(1)A��B��Ӧ�����ֱ�Ϊ___��___��
(2)��A. B�ֱ���4����λ/���3����λ/����ٶ�������У������A. B���1����λ����?
(3)��A. B��(2)�е��ٶ�ͬʱ�����˶�����P��ԭ��O��7����λ/����ٶ������˶����Ƿ���ڳ���m��ʹ��4AP+3OBmOPΪ��ֵ�������������mֵ�Լ������ֵ���������ڣ���˵�����ɡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�����һ��ÿ���۸�Ϊ100Ԫ������Ʒ�����̳��������֣����۵���x(Ԫ/��)��ÿ��������y(��)֮��������ͼ��ʾ�Ĺ�ϵ��

(1)���y��x֮��ĺ�����ϵʽ��
(2)д��ÿ�������W�����۵���x֮��ĺ�����ϵʽ���������̳������ˣ��Ὣ�ۼ۶�Ϊ���٣�����֤ÿ���õ����������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ִ���B����ÿСʱ50������ٶ�����ƫ��30���������ٺ��У���B���۲����Aλ����ƫ��75�������ϣ��ִ����а�Сʱ����C������C���۲����Aλ�ڱ�ƫ��60�������ϣ���C�������A�ľ����ǣ����������
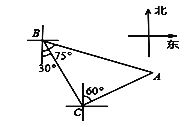
A.50B.25C.25![]() D.25
D.25![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ��������֣�
���ڣ���5![]() ��+����9
��+����9![]() ��+17
��+17![]() +����3
+����3![]() ��
��
�������¼��㣺
ԭʽ=[����5��+����![]() ��]+[����9��+����
��]+[����9��+����![]() ��]+��17+
��]+��17+![]() ��+[����3��+����
��+[����3��+����![]() ��]
��]
=[��һ5��+����9��+17+��һ3��]+[����![]() ��+����
��+����![]() ��+
��+![]() +����
+����![]() ��]=0+����1
��]=0+����1![]() ��
��
=��1![]()
�������ַ����в�����㿴������
��������ķ�����������㣺����1![]() ��+����2000
��+����2000![]() ��+4000
��+4000![]() +����1999
+����1999![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�D��BC�ߵ��е㣬�ֱ��B��C������AD�Ĵ��ߣ�����ֱ�ΪE��F������BF��CE��
��1����֤���ı���BECF��ƽ���ı��Σ�
��2������֪��S��ABD��S��ACD����AF��FD���ڲ����Ӹ����ߵ������£�ֱ��д�����ABD����ACD�����ȵ����������Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ���ı���![]() �У���E�DZ�AB���е㣬�ӳ�DE��CB���ӳ����ڵ�F��
�У���E�DZ�AB���е㣬�ӳ�DE��CB���ӳ����ڵ�F��
��1����֤��![]() ��
��
��2����![]() ������EC����
������EC����![]() �Ķ�����__________________
�Ķ�����__________________

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A��4��3���Ƿ���������y=![]() �ڵ�һ����ͼ����һ�㣬����OA����A��AB��x�ᣬ��ȡAB=OA��B��A�Ҳࣩ������OB��������������y=
�ڵ�һ����ͼ����һ�㣬����OA����A��AB��x�ᣬ��ȡAB=OA��B��A�Ҳࣩ������OB��������������y=![]() ��ͼ���ڵ�P��
��ͼ���ڵ�P��
��1����������y=![]() �ı���ʽ��
�ı���ʽ��
��2�����B�����ꣻ
��3������OAP�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��������ABCD�У�AB=4����BAD=120����ABFΪ�ȱ�������;��E.F�ֱ������εı�BC.CD�ϻ������ҵ�E.F�����B.C.D�غϣ�����E.F�ֱ���BC.CD�ϻ���ʱ�����ı���ABCF�����= ___________�����CEF��������ֵ___________

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com