
【题目】已知:在△ABC和△DEC中,AC=BC,DC=EC,∠ACB=∠ECD=90°.
(1)如图1,当点A、C、D在同一条直线上时,AE与BD的数量关系是 ;
位置关系是 ;
(2)如图2,当点A、C、D不在同一条直线上时,(1)中的结论还成立吗?请说明理由.

【答案】(1)见解析;(2)成立,理由见解析;
【解析】
(1)证明△ACE≌△BCD,得到∠1=∠2,由对顶角相等得到∠3=∠4,所以∠BFE=∠ACE=90°,即可解答;
(2)证明△ACE≌△BCD,得到∠1=∠2,又由∠3=∠4,得到∠BFA=∠BCA=90°,即可解答;
(1)①证明:如图1,
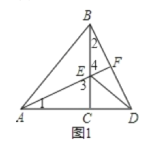
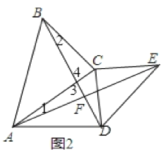
在△ACE和△BCD中,
∵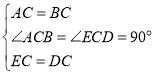 ,
,
∴△ACE≌△BCD,
∴∠1=∠2,AE=BD,
∵∠3=∠4,
∴∠BFE=∠ACE=90°,
∴AE⊥BD;
(2)成立,
证明:如图2,
∵∠ACB=∠ECD,
∴∠ACB+∠ACD=∠ECD+∠ACD,
∴∠BCD=∠ACE,
在△ACE≌△BCD中
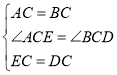 ,
,
∴△ACE≌△BCD,
∴∠1=∠2,AE=BD,
∵∠3=∠4,
∴∠BFA=∠BCA=90°,
∴AF⊥BD.


科目:初中数学 来源: 题型:
【题目】(10分)如图,一小球从斜坡O点处抛出,球的抛出路线可以用二次函数y=﹣x2+4x刻画,斜坡可以用一次函数y=![]() x刻画.
x刻画.
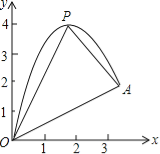
(1)请用配方法求二次函数图象的最高点P的坐标;
(2)小球的落点是A,求点A的坐标;
(3)连接抛物线的最高点P与点O、A得△POA,求△POA的面积;
(4)在OA上方的抛物线上存在一点M(M与P不重合),△MOA的面积等于△POA的面积.请直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC,∠C=90°,AC=12,BC=6,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,要使△ABC和△QPA全等,则AP= ______ .

查看答案和解析>>
科目:初中数学 来源: 题型:
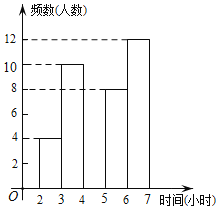
【题目】某中学为了了解学生每周在校体育锻炼时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表,请根据图表信息解答下列问题:
时间(小时) | 频数(人数) | 频率 |
2≤t<3 | 4 | 0.1 |
3≤t<4 | 10 | 0.25 |
4≤t<5 | a | 0.15 |
5≤t<6 | 8 | b |
6≤t<7 | 12 | 0.3 |
合计 | 40 | 1 |
(1)表中的a= ,b= ;
(2)请将频数分布直方图补全;
(3)若该校共有1200名学生,试估计全校每周在校参加体育锻炼时间至少有4小时的学生约为多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE =∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=________度;
(2)设![]() ,
,![]() .
.
①如图2,当点在线段BC上移动,则![]() ,
,![]() 之间有怎样的数量关系?请说明理由;
之间有怎样的数量关系?请说明理由;
②当点在直线BC上移动,则![]() ,
,![]() 之间有怎样的数量关系?请直接写出你的结论.
之间有怎样的数量关系?请直接写出你的结论.




查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市居民使用自来水按照如下标准收费:若每户月用水不超过12m3,按a元/m3收费;若超过12m3,但不超过20m3,则超过的部分按1.5a元/m3收费;若超过20m3超过的部分按2a元/m3收费

(1)把相应的收费金额填在表格里;
(2)已知壮壮家上个月用水量14m3,交水费45元,求a的值;
(3)在(2)的条件下,壮壮妈妈开了一个面馆,工商部门规定:商业用水的价格按照居民用水价格提高50%收取,壮壮妈妈的面馆预计本月用水量28m3,求壮壮妈妈的面馆本月的水费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】荆州古城是闻名遐迩的历史文化名城,“五一”期间相关部门对到荆州观光游客的出行方式进行了随机抽样调查,整理后绘制了两幅统计图(尚不完整).根据图中信息,下列结论错误的是( )
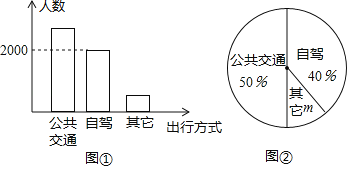
A. 本次抽样调查的样本容量是5000
B. 扇形图中的m为10%
C. 样本中选择公共交通出行的有2500人
D. 若“五一”期间到荆州观光的游客有50万人,则选择自驾方式出行的有25万人
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com