
����Ŀ��ij�о���ʹ������ˮ�������±��շѣ���ÿ������ˮ������12m3����aԪ/m3�շѣ�������12m3����������20m3�����IJ��ְ�1.5aԪ/m3�շѣ�������20m3�����IJ��ְ�2aԪ/m3�շ�

��1������Ӧ���շѽ�����ڱ����
��2����֪׳׳���ϸ�����ˮ��14m3����ˮ��45Ԫ����a��ֵ��
��3���ڣ�2���������£�׳׳���迪��һ����ݣ����̲��Ź涨����ҵ��ˮ�ļ۸��վ�����ˮ�۸����50%��ȡ��׳׳��������Ԥ�Ʊ�����ˮ��28m3����׳׳�������ݱ��µ�ˮ�ѣ�
���𰸡���1������������2��3����3��180Ԫ
��������
��1�������ܼ�=��������������շѱ������������ˮ��Ϊ26m3ʱ���շѽ�
��2������׳׳���ϸ�����ˮ��14m3�ҽ�ˮ��45Ԫ�����ɵó�����a��һԪһ�η��̣���֮���ɵó����ۣ�
��3�������ܼ�=��������������շѱ�����ҵ��ˮ�ļ۸��վ�����ˮ�۸����50%��ȡ���������׳׳�������ݱ��µ�ˮ�ѣ�
�⣺��1��12a+��20-12����1.5a+��26-20����2a=36a��Ԫ����
�ʴ�Ϊ��36a��

��2�������⣬�ã�12a+��14-12����1.5a=45��
��ã�a=3��
��3��[12��3+��20-12����1.5��3+��28-20����2��3]����1+50%��=180��Ԫ����
��׳׳�������ݱ��µ�ˮ��Ϊ180Ԫ��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������㼰�ж���ȷ���ǣ�������
A. ��5��![]() �£���
�£���![]() ����5=1
����5=1
B. ���̣�x2+x��1��x+3=1���ĸ�������
C. ��a��5673=103��a��103=b����a��b=![]()
D. �������ԣ�m2+1��m����ƽ��ֱ������ϵ�ж�Ӧ�ĵ�һ���ڵ�һ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����˶���ǰϦ��������ѧ���Ṻ������������Ϊ��Ʒ��������10�������15��������3000Ԫ���ҹ���һ������ȹ���һ������50Ԫ��
��1������һ������һ������������Ԫ��
��2������ѧУ�ƻ������������������10����ǡ���̳��ڸ��������������ۣ����������ۣ����˴ι�����������ܷ��ò�����1050Ԫ�������ɹ�����ٸ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ABC����DEC�У�AC=BC��DC=EC����ACB=��ECD=90����
��1����ͼ1������A��C��D��ͬһ��ֱ����ʱ��AE��BD��������ϵ�� ��
λ�ù�ϵ�� ��
��2����ͼ2������A��C��D����ͬһ��ֱ����ʱ��(1)�еĽ��ۻ���������˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��CΪ�߶�AE��һ���㣨�����A��E�غϣ�����AEͬ��ֱ�����������ABC����������CDE��AD��BE���ڵ�O��AD��BC���ڵ�P��BE��CD���ڵ�Q������PQ������������ۣ�
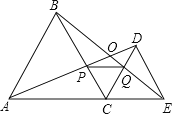
��AD=BE��
��PQ��AE��
��EQ=DP��
�ܡ�AOB=60�㣻
�ݵ�CΪAE�е�ʱ��S��BPQ��S��CDE=1��3�����к�����Ľ����У�������
A.�٢ڢ�B.�٢ڢۢ�C.�٢ڢۢ�D.�٢ڢܢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����⣺
��ͼ�٣���C���߶�AB�ֳ������֣���![]() �����CΪ�߶�AB�Ļƽ�ָ�㣮
�����CΪ�߶�AB�Ļƽ�ָ�㣮
ij�о�ѧϰС�飬�ɻƽ�ָ�����뵽���ƽ�ָ��������Ӷ��������ƽ�ָ������Ķ��壺ֱ��l��һ�����ΪS��ͼ�ηֳ������֣��������ֵ�����ֱ�ΪS1��S2�����![]() ����ô��ֱ��lΪ��ͼ�εĻƽ�ָ��ߣ�
����ô��ֱ��lΪ��ͼ�εĻƽ�ָ��ߣ�
��������
��ͼ�ڣ�����ABC�У���֪D��AB�Ļƽ�ָ�㣮
(1)�о�С����룺ֱ��CD����ABC�Ļƽ�ָ��ߣ�����Ϊ����Ϊʲô��
(2)����˵���������ε������Ƿ�Ҳ�Ǹ������εĻƽ�ָ��ߣ�
(3)�о�С��̽�����֣�����C��ֱ�߽�AB�ڵ�E������D��DF��CE����AC�ڵ�F������EF(��ͼ��)����ֱ��EFҲ����ABC�Ļƽ�ָ��ߣ�����˵�����ɣ�
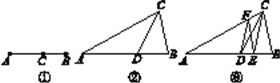
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����߳�Ϊ ![]() ��������
�������� ![]() ��һ��
��һ�� ![]() ��ֱ�DZ߷ֱ���
��ֱ�DZ߷ֱ��� ![]() ��
�� ![]() ��
�� ![]() ��һ��
��һ�� ![]() �غϣ�������
�غϣ������� ![]() ��ÿ��
��ÿ�� ![]() ����λ���ȵ��ٶ���
����λ���ȵ��ٶ��� ![]() ���������˶�������
���������˶������� ![]() �͵�
�͵� ![]() �غ�ʱ������ֹͣ�˶����������ε��˶�ʱ��Ϊ
�غ�ʱ������ֹͣ�˶����������ε��˶�ʱ��Ϊ ![]() �룬������
�룬������ ![]() ��
�� ![]() �ص��������ΪS����S����
�ص��������ΪS����S���� ![]() �ĺ���ͼ��Ϊ�� ��
�ĺ���ͼ��Ϊ�� ��
A. 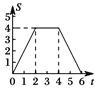 B.
B. 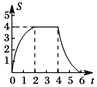 C.
C.  D.
D. 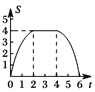
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����⣺
�������߶εij��ȿ������߶ζ˵��ʾ�������м�������õ�������ͼ���߶�AB��1��0������1�����߶� BC��2��2��0���߶� AC��3��2������1������
�������ϵ�M��N���������ֱ�Ϊ��9��1�����߶�MN�� ��
�������ϵ�E��F���������ֱ�Ϊ��6�ͩ�3�����߶�EF�� ��
�������ϵ�������֮��ľ���Ϊ5������һ�����ʾ����Ϊ2������һ�����ʾ����Ϊm����m��
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
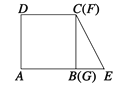
����Ŀ����ͼ1��ֱ��AM��AN��ABƽ�֡�MAN������B��BC��BA��AN�ڵ�C������E��Dͬʱ��A����������ж���E��2cm/s���ٶ�������AN�����˶�������D��1cm/s���ٶ��˶�����֪AC��6cm���趯��D��E���˶�ʱ��Ϊt��
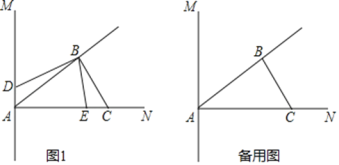
��1������D������AM���˶�ʱ����S��ADB��S��BEC��2��1�������D��E���˶�ʱ��t��ֵ��
��2��������D��ֱ��AM���˶���E������AN�˶������У��Ƿ����ij��ʱ��t��ʹ�á�ADB���BECȫ�ȣ������ڣ������ʱ��t��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com