
【题目】阅读理解:
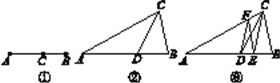
如图①,点C将线段AB分成两部分,若![]() ,则点C为线段AB的黄金分割点.
,则点C为线段AB的黄金分割点.
某研究学习小组,由黄金分割点联想到“黄金分割线”,从而给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1,S2,如果![]() ,那么称直线l为该图形的黄金分割线.
,那么称直线l为该图形的黄金分割线.
问题解决:
如图②,在△ABC中,已知D是AB的黄金分割点.
(1)研究小组猜想:直线CD是△ABC的黄金分割线,你认为对吗?为什么?
(2)请你说明:三角形的中线是否也是该三角形的黄金分割线?
(3)研究小组探究发现:过点C作直线交AB于点E,过点D作DF∥CE,交AC于点F,连接EF(如图③),则直线EF也是△ABC的黄金分割线.请你说明理由.
【答案】(1)对.理由见解析;(2)三角形的中线不是该三角形的黄金分割线.(3)直线EF也是△ABC的黄金分割线.
【解析】(1)根据黄金分割的定义得![]() ,再根据三角形面积公式得到
,再根据三角形面积公式得到![]() ,
,![]() ,所以
,所以![]() ,然后根据黄金直线的定义得直线CD是△ABC的黄金分割线;
,然后根据黄金直线的定义得直线CD是△ABC的黄金分割线;
(2)根据三角形中线的性质和三角形面积公式得到![]() ,而
,而![]() <1,由此可根据黄金直线的定义判断三角形的中线不是该三角形的黄金分割线;
<1,由此可根据黄金直线的定义判断三角形的中线不是该三角形的黄金分割线;
(3)根据两平行线之间的距离定值,得到S△FDE=S△FDC,S△DEC=S△FEC,则S△AEF=S△ADC,S四边形BEFC=S△BDC,然后由![]() 得到
得到![]() ,则可根据黄金直线的定义判断直线EF也是△ABC的黄金分割线.
,则可根据黄金直线的定义判断直线EF也是△ABC的黄金分割线.
(1)直线CD是△ABC的黄金分割线.理由如下:
∵点D是AB的黄金分割点,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴直线CD是△ABC的黄金分割线;
(2)∵三角形的中线把AB分成相等的两条线段,即AD=BD,
∴![]() ,
,![]() ,
,
∴三角形的中线不是该三角形的黄金分割线;
(3)∵DF∥CE,
∴S△FDE=S△FDC,S△DEC=S△FEC,
∴S△AEF=S△ADC,S四边形BEFC=S△BDC,
∵![]() ,
,
∴![]() ,
,
∴直线EF是△ABC的黄金分割线.


科目:初中数学 来源: 题型:
【题目】联想三角形外心的概念,我们可引入如下概念。
定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心。
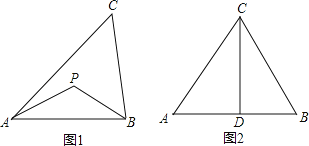
举例:如图1,若PA=PB,则点P为△ABC的准外心。
应用:如图2,CD为等边三角形ABC的高,准外心P在高CD上,且PD=![]() AB,求∠APB的度数。
AB,求∠APB的度数。
探究:已知△ABC为直角三角形,斜边BC=5,AB=3,准外心P在AC边上,试探究PA的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE =∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=________度;
(2)设![]() ,
,![]() .
.
①如图2,当点在线段BC上移动,则![]() ,
,![]() 之间有怎样的数量关系?请说明理由;
之间有怎样的数量关系?请说明理由;
②当点在直线BC上移动,则![]() ,
,![]() 之间有怎样的数量关系?请直接写出你的结论.
之间有怎样的数量关系?请直接写出你的结论.




查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市居民使用自来水按照如下标准收费:若每户月用水不超过12m3,按a元/m3收费;若超过12m3,但不超过20m3,则超过的部分按1.5a元/m3收费;若超过20m3超过的部分按2a元/m3收费

(1)把相应的收费金额填在表格里;
(2)已知壮壮家上个月用水量14m3,交水费45元,求a的值;
(3)在(2)的条件下,壮壮妈妈开了一个面馆,工商部门规定:商业用水的价格按照居民用水价格提高50%收取,壮壮妈妈的面馆预计本月用水量28m3,求壮壮妈妈的面馆本月的水费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() ,OB、OM、ON,是
,OB、OM、ON,是![]() 内的射线.
内的射线.
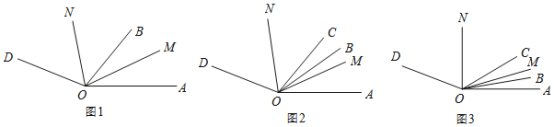
(1)如图 1,若 OM 平分 ![]() , ON平分
, ON平分![]() .当射线OB 绕点O 在
.当射线OB 绕点O 在![]() 内旋转时,
内旋转时,![]() = 度.
= 度.
(2)OC也是![]() 内的射线,如图2,若
内的射线,如图2,若![]() ,OM平分
,OM平分![]() ,ON平分
,ON平分![]() ,当射线OB绕点O在
,当射线OB绕点O在![]() 内旋转时,求
内旋转时,求![]() 的大小.
的大小.
(3)在(2)的条件下,当射线OB从边OA开始绕O点以每秒![]() 的速度逆时针旋转t秒,如图3,若
的速度逆时针旋转t秒,如图3,若![]() ,求t的值.
,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在求1+2+22+23+24+25+26的值时,小明发现:从第二个加数起每一个加数都是前一个加数的2倍,于是他设:S=1+2+22+23+24+25+26 为①式,然后在①式的两边都乘以2,得:2S=2+22+23+24+25+26+27 为②式;②﹣ ①得2S﹣S=27﹣1,S=27﹣1,即1+2+22+23+24+25+26=27﹣1.
(1)求1+3+32+33+34+35+36的值;
(2)求1+a+a2+a3+…+a2016(a≠0且a≠1)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
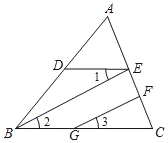
【题目】已知:如图,BE∥GF,∠1=∠3,∠DBC=70°,求∠EDB的大小.
阅读下面的解答过程,并填空(理由或数学式)
解:∵BE∥GF(已知)
∴∠2=∠3( )
∵∠1=∠3( )
∴∠1=( )( )
∴DE∥( )( )
∴∠EDB+∠DBC=180°( )
∴∠EDB=180°﹣∠DBC(等式性质)
∵∠DBC=( )(已知)
∴∠EDB=180°﹣70°=110°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com