已知关于x的一元二次方程x2+(m+3)x+m+1=0.
(1)求证:无论m取何值,原方程总有两个不相等的实数根;
(2)当m为何整数时,原方程的根也是整数.
(1)证明:△=(m+3)
2-4(m+1)=m
2+6m+9-4m-4=m
2+2m+5=(m+1)
2+4,
∵(m+1)
2≥0,
∴(m+1)
2+4>0,
则无论m取何实数时,原方程总有两个不相等的实数根;
(2)解:关于x的一元二次方程x
2+(m+3)x+m+1=0,
利用公式法解得:x=
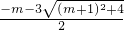
,
要使原方程的根是整数,必须使得(m+1)
2+4是完全平方数,
设(m+1)
2+4=a
2,变形得:(a+m+1)(a-m-1)=4,
∵a+m+1和a-m-1的奇偶性相同,
可得
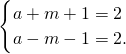
或
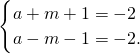
,
解得:
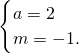
或
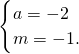
,
将m=-1代入x=
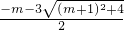
,得x
1=-2,x
2=0符合题意,
∴当m=-1时,原方程的根是整数.
分析:(1)表示出根的判别式,配方后得到根的判别式大于0,进而确定出方程总有两个不相等的实数根;
(2)由(1)得到方程有两个不相等的实数根,利用求根公式表示出解,要使原方程的根是整数,必须使得(m+1)
2+4是完全平方数,设(m+1)
2+4=a
2,变形得:(a+m+1)(a-m-1)=4,由a+m+1和a-m-1的奇偶性相同,列出方程组,求出方程组的解得到a与m的值,代入解中检验即可得到满足题意m的值.
点评:此题考查了根的判别式,以及求根公式,根的判别式的值大于0,方程有两个不相等的实数根;根的判别式的值等于0,方程有两个相等的实数根;根的判别式的值小于0,方程没有实数根.

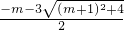 ,
,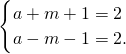 或
或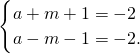 ,
,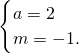 或
或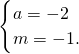 ,
,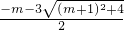 ,得x1=-2,x2=0符合题意,
,得x1=-2,x2=0符合题意,

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案 .
. .
.