
【题目】已知函数f(x)=1+2cosxcos(x+3φ)是偶函数,其中φ∈(0, ![]() ),则下列关于函数g(x)=cos(2x﹣φ)的正确描述是( )
),则下列关于函数g(x)=cos(2x﹣φ)的正确描述是( )
A.g(x)在区间[﹣ ![]() ]上的最小值为﹣1.
]上的最小值为﹣1.
B.g(x)的图象可由函数f(x)向上平移2个单位,在向右平移 ![]() 个单位得到.
个单位得到.
C.g(x)的图象可由函数f(x)的图象先向左平移 ![]() 个单位得到.
个单位得到.
D.g(x)的图象可由函数f(x)的图象先向右平移 ![]() 个单位得到.
个单位得到.
【答案】C
【解析】解:∵函数f(x)=1+2cosxcos(x+3φ)是偶函数,其中φ∈(0, ![]() ), ∴3φ=π,φ=
), ∴3φ=π,φ= ![]() ,∴f(x)=1+2cosxcos(x+π)=1﹣2cos2x=﹣cos2x=cos(π﹣2x)=cos(2x﹣π),
,∴f(x)=1+2cosxcos(x+π)=1﹣2cos2x=﹣cos2x=cos(π﹣2x)=cos(2x﹣π),
∴函数g(x)=cos(2x﹣φ)=cos(2x﹣ ![]() ),
),
故函数f(x)的图象先向左平移 ![]() 个单位得到y=cos[2(x+
个单位得到y=cos[2(x+ ![]() )﹣π]=cos(2x﹣
)﹣π]=cos(2x﹣ ![]() )=g(x)的图象,
)=g(x)的图象,
故选:C.
【考点精析】利用函数y=Asin(ωx+φ)的图象变换对题目进行判断即可得到答案,需要熟知图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象.
的图象.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2+bx+2过B(﹣2,6),C(2,2)两点.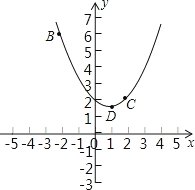
(1)试求抛物线的解析式;
(2)记抛物线顶点为D,求△BCD的面积;
(3)若直线y=﹣ ![]() x向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点,求b的取值范围.
x向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点,求b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A、B的坐标分别为(8,0)、(0,2 ![]() ),C是AB的中点,过点C作y轴的垂线,垂足为D,动点P从点D出发,沿DC向点C匀速运动,过点P作x轴的垂线,垂足为E,连接BP、EC.当BP所在直线与EC所在直线第一次垂直时,点P的坐标为
),C是AB的中点,过点C作y轴的垂线,垂足为D,动点P从点D出发,沿DC向点C匀速运动,过点P作x轴的垂线,垂足为E,连接BP、EC.当BP所在直线与EC所在直线第一次垂直时,点P的坐标为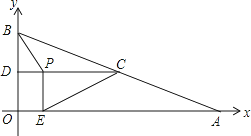
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校准备组织师生共60人,从南靖乘动车前往厦门参加夏令营活动,动车票价格如表所示:(教师按成人票价购买,学生按学生票价购买).
运行区间 | 成人票价(元/张) | 学生票价(元/张) | ||
出发站 | 终点站 | 一等座 | 二等座 | 二等座 |
南靖 | 厦门 | 26 | 22 | 16 |
若师生均购买二等座票,则共需1020元.
(1)参加活动的教师有人,学生有人;
(2)由于部分教师需提早前往做准备工作,这部分教师均购买一等座票,而后续前往的教师和学生均购买二等座票.设提早前往的教师有x人,购买一、二等座票全部费用为y元.
①求y关于x的函数关系式;
②若购买一、二等座票全部费用不多于1032元,则提早前往的教师最多只能多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通过随机询问某地100名高中学生在选择座位时是否挑同桌,得到如下2×2列联表:
男生 | 女生 | 合计 | |
挑同桌 | 30 | 40 | 70 |
不挑同桌 | 20 | 10 | 30 |
总计 | 50 | 50 | 100 |
(Ⅰ)从这50名男生中按是否挑同桌采取分层抽样的方法抽取一个容量为5的样本,现从这5人中随机选取3人做深度采访,求这3名学生中至少有2名要挑同桌的概率;
(Ⅱ)根据以上2×2列联表,是否有95%以上的把握认为“性别与在选择座位时是否挑同桌”有关?
下面的临界值表供参考:
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知过点A(0,1)的椭圆C: ![]() +
+ ![]() =1(a>b>0)的左右焦点分别为F1、F2 , B为椭圆上的任意一点,且
=1(a>b>0)的左右焦点分别为F1、F2 , B为椭圆上的任意一点,且 ![]() |BF1|,|F1F2|,
|BF1|,|F1F2|, ![]() |BF2|成等差数列.
|BF2|成等差数列.
(1)求椭圆C的标准方程;
(2)直线l:y=k(x+2)交椭圆于P,Q两点,若点A始终在以PQ为直径的圆外,求实数k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知F1、F2分别为双曲线C: ![]() =1的左、右焦点,P为双曲线C右支上一点,且|PF1|=2|PF2|,则△PF1F2外接圆的面积为( )
=1的左、右焦点,P为双曲线C右支上一点,且|PF1|=2|PF2|,则△PF1F2外接圆的面积为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四棱锥P﹣ABCD,底面ABCD为矩形,点E,F在侧棱PA,PB上且PE=2EA,PF=2FB,点M为四棱锥内任一点,则M在平面EFCD上方的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com