
【题目】已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
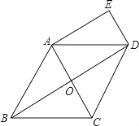
(1)求证:四边形AODE是矩形;
(2)若AB=4,∠BCD=120°,求四边形AODE的面积.
【答案】(1)证明见解析(2)![]()
【解析】试题分析:(1)由DE∥AC和AE∥BD得到:四边形AODE是平行四边形,由菱形ABCD中AC和BD是对角线得到:AC⊥BD,综合以上两点可得平行四边形AODE是矩形;(2)由∠BCD=120°,AB∥CD得:∠ABC=180°﹣120°=60°,又因为AB=BC得:△ABC是等边三角形,所以OA=![]() ×4=2,在菱形ABCD中,AC⊥BD,由勾股定理OB=
×4=2,在菱形ABCD中,AC⊥BD,由勾股定理OB=![]() ,由四边形ABCD是菱形得:OD=OB=
,由四边形ABCD是菱形得:OD=OB=![]() ,所以四边形AODE的面积=OAOD=2
,所以四边形AODE的面积=OAOD=2![]() (或
(或![]() );
);
试题解析:
(1)∵DE∥AC,AE∥BD,
∴四边形AODE是平行四边形,
∵在菱形ABCD中,AC⊥BD,
∴平行四边形AODE是矩形,
故,四边形AODE是矩形;
(2)∵∠BCD=120°,AB∥CD,
∴∠ABC=180°﹣120°=60°,
∵AB=BC,
∴△ABC是等边三角形,
∴OA=![]() ×4=2,
×4=2,
∵在菱形ABCD中,AC⊥BD
∴由勾股定理OB=![]()
∵四边形ABCD是菱形,
∴OD=OB=![]() ,
,
∴四边形AODE的面积=OAOD=2![]() (或
(或![]() )
)


科目:初中数学 来源: 题型:
【题目】如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与直线CD的位置关系,并说明理由;
(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;
(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?若不变,请求出其值;若变化,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆有50个房间供游客居住,当每个房间定价120元时,房间会全部住满,当每个房间每天的定价每增加10元时,就会有一个房间空闲。如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用,设每个房间定价增加10 x元(x为整数)。
(1)(2分)直接写出每天游客居住的房间数量y与x的函数关系式。
(2)(4分)设宾馆每天的利润为W元,当每间房价定价为多少元时,宾馆每天所获利润最大,最大利润是多少?
(3)(4分)某日,宾馆了解当天的住宿的情况,得到以下信息:①当日所获利润不低于5000元,②宾馆为游客居住的房间共支出费用没有超过600元,③每个房间刚好住满2人。问:这天宾馆入住的游客人数最少有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的方程(k-1)x2+2kx+2=0
(1)求证:无论k为何值,方程总有实数根。
(2)设x1,x2是方程(k-1)x2+2kx+2=0的两个根,记S=![]() +
+![]() + x1+x2,S的值能为2吗?若能,求出此时k的值。若不能,请说明理由。
+ x1+x2,S的值能为2吗?若能,求出此时k的值。若不能,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行四边形ABCD中,E,F是对角线BD上的两点, 如果添加一个条件使△ABE≌△CDF,则添加的条件不能是( )

A. AE=CF B. BE=FD C. BF=DE D. ∠1=∠2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)若△ABC经过平移后得到△A1B1C1,已知点C1的坐标为(4,0),写出顶点A1,B1的坐标,并画出△A1B1C1;
(2)若△ABC和△A2B2C2关于原点O成中心对称图形,写出△A2B2C2的各顶点的坐标;
(3)将△ABC绕着点O按顺时针方向旋转90°得到△A3B3C3,写出△A3B3C3的各顶点的坐标,并画出△A3B3C3.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com