
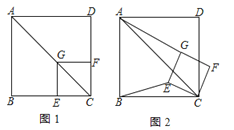
【题目】如图,已知点G在正方形ABCD的对角线AC上,GE⊥BC,GF⊥CD,垂足分别为点E,F.
(1)求证:四边形CEGF是正方形;
(2)将正方形CEGF绕点C顺时针旋转![]() ,如图所示,线段BE与DF是否相等?为什么?
,如图所示,线段BE与DF是否相等?为什么?
科目:初中数学 来源: 题型:
【题目】某中学举行演讲比赛,七年级(1)班、(2)班根据初赛成绩各选出5名选手参加复赛,两个班所选出的5名选手的复赛成绩如下面条形统计图所示.
平均分(分) | 中位数(分) | 众数(分) | 方差 | |
(1)班 | 85 | a | 85 | 70 |
(2)班 | 85 | 80 | b | c |
(1)根据条形统计图中的信息,求上表中a,b,c的值;
(2)请你分析说明哪个班级的复赛成绩较好.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从边长为a的正方形中剪掉一个边长为b的正方形(如图①),然后将剩余部分拼成一个长方形(如图②).

(1) 上述操作能验证的等式是__________________;
(2) 应用你从(1)得出的等式,完成下列各题:
①已知x24y2=12,x+2y=4,求x2y的值.
②计算:(1![]() )(1
)(1![]() )(1
)(1![]() )…(1
)…(1![]() )(1
)(1![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
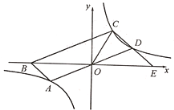
【题目】如图,在平面直角坐标系中,平行四边形ABCD的边AD经过O点,A、C、D三点都在反比例函数![]() 的图像上,B点在
的图像上,B点在![]() 轴的负半轴上,延长CD交
轴的负半轴上,延长CD交![]() 轴于点E,连接CO.
轴于点E,连接CO.
若C(1,2),D(2,1),则![]() 为_______.
为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
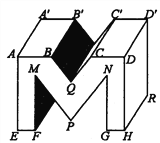
【题目】如图所示,在书写艺术字时,常常运用画“平行线段”这种基本作图方法,此图是在书写字“M”:
(1)请从正面,上面,右侧三个不同方向上各找出一组平行线段,并用字母表示出来;
(2)EF与A′B′有何位置关系?CC′与DH有何位置关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
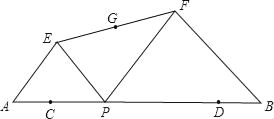
【题目】如图,已知AB=12,点C,D在AB上,且AC=DB=2,点P从点C沿线段CD向点D运动(运动到点D停止),以AP、BP为斜边在AB的同侧画等腰Rt△APE和等腰Rt△PBF,连接EF,取EF的中点G,①△EFP的外接圆的圆心为点G;②四边形AEFB的面积不变;③EF的中点G移动的路径长为4;④△EFP的面积的最小值为8.以上说法中正确的有_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
2019年4月底,“百年器象——清华大学科学博物馆筹备展”上展出了一件清华校友捐赠的历史文物“Husun型六分仪”(图①),它见证了中国人民解放军海军的发展历程.六分仪是测量天体高度的手提式光学仪器,它的主要原理是几何光学中的反射定律.观察测者手持六分仪(图②)按照一定的观测步骤(图③显示的是其中第6步)读出六分仪加油弧标尺上的刻度,再经过一定计算得出观察测点的地理坐标.

请大家证明在使用六分仪测量时用到的一个重要结论(两次反射原理).
已知:在图④所示的“六分仪原理图”中,所观测星体记为![]() ,两个反射镜面位于
,两个反射镜面位于![]() 两处,
两处,![]() 处的镜面的在直线
处的镜面的在直线![]() 自动与
自动与![]() 刻度线
刻度线![]() 保持平行(即
保持平行(即![]() ),并与
),并与![]() 处的镜面所在直线
处的镜面所在直线![]() 交于点
交于点![]() ,
,![]() 所在直线与水平线
所在直线与水平线![]() 交于点
交于点![]() ,六分仪上刻度线
,六分仪上刻度线![]() 与
与![]() 刻度线的夹角
刻度线的夹角![]() ,观测角为
,观测角为![]() .(请注意小贴士中的信息)
.(请注意小贴士中的信息)
求证:![]()

请在答题卡上完成对紫结论的以下填空及后续证明过程(后续证明无需标注理由).
证明:∵![]()
∴![]() ( )
( )
∵![]()
∴![]() ( )
( )
∵![]() ( )
( )
又∵![]() (小贴士已知),
(小贴士已知),
∴![]() .
.
∵![]() 是
是![]() 的外角,
的外角,
∴![]() ( ).
( ).
即![]() .
.
补全证明过程:(请在答题卡上完成)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com