Question

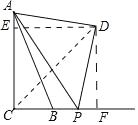
【题目】如图，Rt△ACB中，∠C＝90°，AC＝5cm，BC＝2cm，点P从B点出发以1cm/s的速度沿CB延长线运动，运动时间为t秒．以AP为斜边在其上方构造等腰直角△APD．当t＝1秒时，则CD＝_____cm，当D运动的路程为4cm时，则P运动时间t＝_____秒．

Answer 1

【答案】4 8

【解析】

连接CD，作DF⊥CB于F，DE⊥CA于E．首先证明AC+CB＝CD，延长即可解决问题；

解：连接CD，作DF⊥CB于F，DE⊥CA于E．

∵DA＝DP，∠ADP＝90°，

∴∠DAP＝∠DPA＝45°，

∵∠ACP+∠ADP＝180°，

∴A，C，P，D四点共圆，

∴∠ACD＝∠APD＝45°，

∴∠ACD＝∠DCF，

∵DE⊥CA，DF⊥CF，

∴DE＝DF，

∵∠EDF＝∠ADP＝90°，

∴∠ADE＝∠PDF，

∵∠DEA＝∠DFP＝90°，

∴△DEA≌△DFP（ASA），

∴AE＝DF，

∵CD＝CD，DE＝DF，

∴Rt△CDE≌Rt△CDF（HL），

∴CE＝DF，

∴四边形ECFD是正方形，

∴AC+CP＝EC+AE+CF﹣PF＝2EC＝CD，

∵t＝1s时，AC＝5cm，CP＝3cm，

∴CD＝＝4（cm），

当t＝0时，CD＝＝，

当D运动的路程为4cm时，CD＝4+＝，

∵AC+CP＝CD，

∴5+CP＝15，

∴CP＝10，

∴PB＝8，t＝8.

故答案为：4；8．