
【题目】如图,在正方形![]() 中,边长
中,边长![]() 为
为![]() ,菱形
,菱形![]() 的三个顶点
的三个顶点![]() 分别在正方形的边
分别在正方形的边![]() 上
上![]() 连接
连接![]() ,则
,则![]() 的面积等于_____.
的面积等于_____.
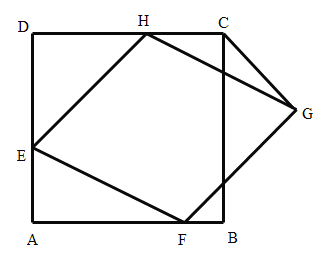
【答案】2
【解析】
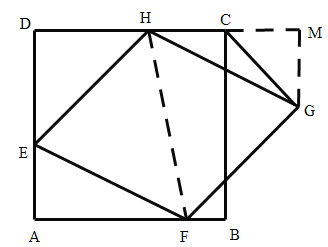
如图,连接HF,过点G作GM⊥DC交DC延长线于点M,根据正方形的性质及平行线的性质得到∠AFH=∠MHF,根据菱形的性质得到∠EFH=∠GHF,进而证明∠AFE=∠MHG,从而证明△AFE≌△MHG(AAS),得到MG=2,计算出HC,再根据三角形的面积公式即可解答.
解:如图,连接HF,过点G作GM⊥DC交DC延长线于点M,则∠M=90°,
∵四边形ABCD是正方形,边长为5,
∴AD=DC=5,∠A=90°,![]() ,
,
∴∠AFH=∠MHF,
∵四边形![]() 是菱形,
是菱形,
∴EF=HG,![]() ,
,
∴∠EFH=∠GHF,
∴∠AFH-∠EFH =∠MHF-∠GHF,
即∠AFE=∠MHG,
在△AFE与△MHG中,
∠A=∠M=90°,∠AFE=∠MHG,EF=HG,
∴△AFE≌△MHG(AAS),
∴AE=MG=2,
∵DH=3,
∴HC=5-3=2,
∴S△HCG=![]() ,
,
故答案为:2.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】如图1,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90°
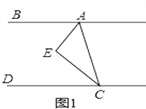
(1)请判断AB与CD的位置关系并说明理由;
(2)如图2,在(1)的结论下,当∠E=90°保持不变,移动直角顶点E,使∠MCE=∠ECD,当直角顶点E点移动时,问∠BAE与∠MCD是否存在确定的数量关系?

(3)如图3,在(1)的结论下,P为线段AC上一定点,点Q为直线CD上一动点,当点Q在射线CD上运动时(点C除外)∠CPQ+∠CQP与∠BAC有何数量关系? (2、3小题只需选一题说明理由)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,扇形OAB的圆心角为90°,点C,D是弧AB的三等分点,半径OC,OD分别与弦AB交于点E,F,下列说法错误的是( ) 
A.AE=EF=FB
B.AC=CD=DB
C.EC=FD
D.∠DFB=75°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解下列方程时,配方有错误的是( )
A.x2﹣2x﹣99=0化为(x﹣1)2=100
B.x2+8x+9=0化为(x+4)2=25
C.2t2﹣7t﹣4=0化为(t﹣ ![]() )2=
)2= ![]()
D.3x2﹣4x﹣2=0化为(x﹣ ![]() )2=
)2= ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把四张形状大小完全相同的小长方形卡片(如图①)不重叠的放在一个底面为长方形(长为m厘米,宽为n厘米)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分的周长和是( )

A. 4m厘米 B. 4n厘米 C. 2(m+n)厘米 D. 4(m-n)厘米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xoy中,A(-1,5)、B(-1,0),C(-4,3).

(1)△ABC的面积是 .
(2)在下图中画出△ABC向下平移2个单位,向右平移5个单位后的△A1B1C1.
(3)写出点A1、B1、C1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E、F、G、H分别是矩形ABCD边AB、BC、CD、DA上的点,且HG与EF交于点I,连接HE、FG,若AB=6,BC=5,EF//AD,HG//AB,则HE+FG的最小值是_____ .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com