
【题目】如图,点A、B、C、D在⊙O上,DE⊥OA,DF⊥OB,垂足分别为E,F,若∠EDF=50°,则∠C的度数为( ) 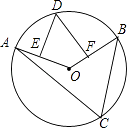
A.40°
B.50°
C.65°
D.130°
 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
【题目】如图,在边长为4的菱形ABCD中,∠A=60°,M是AD边的中点,点N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连接A′C,则线段A′C长度的最小值是 . 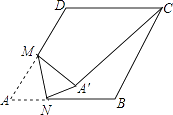
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司在甲地、乙地分别生产了17台、15台同一种型号的机械设备,现要将这些设备全部运往A、B两市,其中运往A市18台、运往B市14台,从甲地运往A、B两市的费用分别为800元/台和500元/台,从乙地运往A、B两市的费用分别为700元/台和600元/台.设甲地运往A市的设备有x台.
(1)请用x的代数式分别表示甲地运往B市、乙地运往A市、乙地运往B市的设备台数;
(2)求出总运费y(元)与x(台) 的函数关系式,并求出自变量的取值范围;
(3)要使总运费不高于20200元,请你帮助该公司设计调配方案,并写出有哪几种方案,哪种方案总运费最小,最小值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名同学进行了6轮投篮比赛,两人的得分情况统计如下:

下列说法不正确的是( )
A. 甲得分的极差小于乙得分的极差 B. 甲得分的中位数大于乙得分的中位数
C. 甲得分的平均数大于乙得分的平均数 D. 乙的成绩比甲的成绩稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△OAB在直角坐标系中的位置如图,点A在第一象限,点B在x轴正半轴上,OA=OB=6,∠AOB=30°.
(1)求点A、B的坐标;
(2)开口向上的抛物线经过原点O和点B,设其顶点为E,当△OBE为等腰直角三角形时,求抛物线的解析式;
(3)设半径为2的⊙P与直线OA交于M、N两点,已知MN=2 ![]() ,P(m,2)(m>0),求m的值.
,P(m,2)(m>0),求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,山坡上有一颗树AB,树底部B点到山脚C点的距离BC为6 ![]() 米,山坡的坡角为30°,小宇在山脚的平地F处测量这棵树的高,点C到测角仪EF的水平距离CF=1米,从E处测得树顶部A的仰角为45°,树底部B的仰角为20°,求树AB的高度.
米,山坡的坡角为30°,小宇在山脚的平地F处测量这棵树的高,点C到测角仪EF的水平距离CF=1米,从E处测得树顶部A的仰角为45°,树底部B的仰角为20°,求树AB的高度.
(参考数值:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)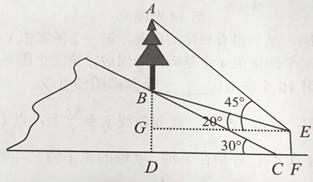
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com