
【题目】如图,山坡上有一颗树AB,树底部B点到山脚C点的距离BC为6 ![]() 米,山坡的坡角为30°,小宇在山脚的平地F处测量这棵树的高,点C到测角仪EF的水平距离CF=1米,从E处测得树顶部A的仰角为45°,树底部B的仰角为20°,求树AB的高度.
米,山坡的坡角为30°,小宇在山脚的平地F处测量这棵树的高,点C到测角仪EF的水平距离CF=1米,从E处测得树顶部A的仰角为45°,树底部B的仰角为20°,求树AB的高度.
(参考数值:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)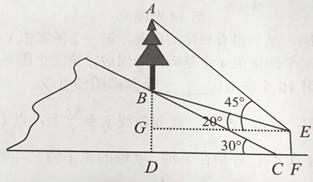
【答案】解:在Rt△BCD中,CD=BC×cos∠BCD=6![]() ×
×![]() =9,
=9,
则DF=CD+CF=10(米),
∵四边形GDFE为矩形,
∴GE=DF=10(米),
∵∠AEG=45°,
∴AG=GE=10(米),
在Rt△BEG中,BG=GE×tan∠BEG≈10×0.36=3.6(米),
则AB=AG-BG=10-3.6=6.4(米).
答:旗杆AB的高度为6.4米.
【解析】根据AB=AG-BG,先求出AG和BG,在Rt△ABG中,∠AEG=45°,则AG=GE=DF=CD+CF,需要求出CD,BC已知,∠BCD的度数已知,可求得;在在Rt△BEG中,∠BEG已知,GE前面已求得,则解答案完成.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,点A、B、C、D在⊙O上,DE⊥OA,DF⊥OB,垂足分别为E,F,若∠EDF=50°,则∠C的度数为( ) 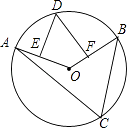
A.40°
B.50°
C.65°
D.130°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A、B两地相距4千米,上午11:00,甲从A地出发步行到B地,11:20乙从B地出发骑自行车到A地,甲乙两人离A地的距离(千米)与甲所用时间(分)之间的关系如图所示,由图中的信息可知,乙到达A地的时间为( )
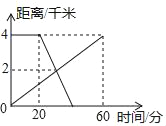
A. 上午11:40 B. 上午11:35 C. 上午11:45 D. 上午11:50
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形A1B1C1D1、A2B2C2D2……按照如图所示的方式放置,点A1、A2、A3、…和点C1、C2、C3、…分别在直线y=kx+b(k>0)和x轴上,已知B1(1,1),B2(3,2),B3(7,4)则B2018的坐标是_____.
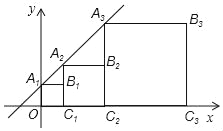
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,lA、lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
(1)B出发时与A相距 千米.
(2)B走了一段路后,自行车发生故障,进行修理,所用的时间是 小时.
(3)B出发后 小时与A相遇.
(4)求出A行走的路程S与时间t的函数关系式.
(5)若B的自行车不发生故障,保持出发时的速度前进, 小时与A相遇,相遇点离B的出发点 千米.在图中表示出这个相遇点C.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 ![]() ABC中,AD平分
ABC中,AD平分 ![]() BAC,按如下步骤作图:
BAC,按如下步骤作图:
第一步,分别以点A、D为圆心,以大于 ![]() AD的长为半径在AD两侧做弧,交于两点M、N;
AD的长为半径在AD两侧做弧,交于两点M、N;
第二步,连接MN分别交AB、AC于点E、F;
第三步,连接DE、DF.
若BD=6,AF=4,CD=3,则BE的长是( ).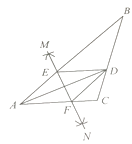
A.2
B.4
C.6
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形 ABCD 中,AB=AD,AC=5,∠DAB=∠DCB=90°, 则四边形 ABCD 的面积为( )
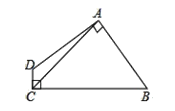
A. 15 B. 14.5 C. 13 D. 12.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2015本溪,第9题,3分)如图,在平面直角坐标系中,直线AB与x轴交于点A(﹣2,0),与x轴夹角为30°,将△ABO沿直线AB翻折,点O的对应点C恰好落在双曲线![]() (
(![]() )上,则k的值为( )
)上,则k的值为( )

A. 4 B. ﹣2 C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com