
【题目】如图,lA、lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
(1)B出发时与A相距 千米.
(2)B走了一段路后,自行车发生故障,进行修理,所用的时间是 小时.
(3)B出发后 小时与A相遇.
(4)求出A行走的路程S与时间t的函数关系式.
(5)若B的自行车不发生故障,保持出发时的速度前进, 小时与A相遇,相遇点离B的出发点 千米.在图中表示出这个相遇点C.

【答案】(1)10;(2)1;(3)3;(4)S=![]() x+10.(5)
x+10.(5)![]() ;
;![]() .
.
【解析】
(1)出发时时间记为0,由此即可确定B出发时与A相距多少千米;
(2)由于自行车发生故障,进行修理,所以S没有改变,由此即可确定修理所用的时间;
(3)若A与B相遇,那么图象有交点,由此根据图象即可确定B出发后多少小时与A相遇;
(4)由于B开始的速度为7.5÷0.5=15千米/小时,那么B的自行车不发生故障,保持出发时的速度前进,根据和A相距10千米可以列出方程求出相遇时间,然后就可以求出相遇点离B的出发点的距离;
(5)可以利用待定系数法确定A行走的路程S与时间t的函数关系式.
(1)∵当t=0时,S=10,
∴B出发时与A相距10千米,
故答案为:10;
(2)1.5﹣0.5=1(小时).
故答案为:1;
(3)观察函数图象,可知:B出发后3小时与A相遇.
故答案为:3;
(4)设A行走的路程S与时间t的函数关系式为S=kt+b(k≠0),
将(0,10),(3,22.5)代入S=kt+b,
得:![]() ,解得:
,解得: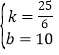 ,
,
∴A行走的路程S与时间t的函数关系式为S=![]() x+10;
x+10;
(5)设若B的自行车不发生故障,则B行走的路程S与时间t的函数关系式为S=mt,
∵点(0.5,7.5)在该函数图象上,
∴7.5=0.5m,
解得:m=15,
∴设若B的自行车不发生故障,则B行走的路程S与时间t的函数关系式为S=15t,
联立两函数解析式成方程组,
得: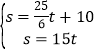 ,解得:
,解得: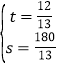 ,
,
∴若B的自行车不发生故障,保持出发时的速度前进,![]() 小时与A相遇,相遇点离B的出发点
小时与A相遇,相遇点离B的出发点![]() 千米,相遇点C的位置如图所示.
千米,相遇点C的位置如图所示.
故答案为:![]() ;
;![]() .
.


科目:初中数学 来源: 题型:
【题目】某公司在甲地、乙地分别生产了17台、15台同一种型号的机械设备,现要将这些设备全部运往A、B两市,其中运往A市18台、运往B市14台,从甲地运往A、B两市的费用分别为800元/台和500元/台,从乙地运往A、B两市的费用分别为700元/台和600元/台.设甲地运往A市的设备有x台.
(1)请用x的代数式分别表示甲地运往B市、乙地运往A市、乙地运往B市的设备台数;
(2)求出总运费y(元)与x(台) 的函数关系式,并求出自变量的取值范围;
(3)要使总运费不高于20200元,请你帮助该公司设计调配方案,并写出有哪几种方案,哪种方案总运费最小,最小值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高节水意识,小申随机统计了自己家7天的用水量,并分析了第3天的用水情况,将得到的数据进行整理后,绘制成如图所示的统计图.(单位:升)
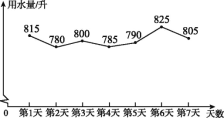
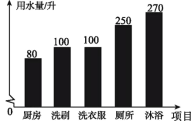
(1)求这7天内小申家每天用水量的平均数和中位数;
(2)求第3天小申家洗衣服的水占这一天总用水量的百分比;
(3)请你根据统计图中的信息,给小申家提出一条全理的节约用水建议,并估算采用你的建议后小申家一个月(按30天计算)的节约用水量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax-2ax-3a(a<0)与x轴交于A、B两点(A在B的左侧),与y轴交于点C,抛物线的对称轴与抛物线交于点P,与直线BC交于点M,且PM= ![]() AB.
AB.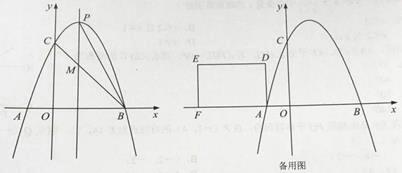
(1)求抛物线的解析式;
(2)点K是x轴正半轴上一点,点A、P关于点K的对称点分别为 ![]() 、
、 ![]() ,连接
,连接 ![]() 、
、 ![]() ,若
,若 ![]()
![]()
![]() ,求点K的坐标;
,求点K的坐标;
(3)矩形ADEF的边AF在x轴负半轴上,边AD在第二象限,AD=2,DE=3.将矩形ADEF沿x轴正方向平移t(t>0)个单位,直线AD、EF分别交抛物线于G、H.问:是否存在实数t,使得以点D、F、G、H为顶点的四边形是平行四边形?若存在,求出t的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
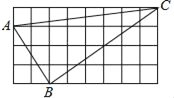
【题目】如图,正方形网格中有△ABC,若小方格边长为1,请你根据所学的知识解答下列问题:
(1)判断△ABC是什么形状?并说明理由.
(2)求△ABC中BC边上的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,山坡上有一颗树AB,树底部B点到山脚C点的距离BC为6 ![]() 米,山坡的坡角为30°,小宇在山脚的平地F处测量这棵树的高,点C到测角仪EF的水平距离CF=1米,从E处测得树顶部A的仰角为45°,树底部B的仰角为20°,求树AB的高度.
米,山坡的坡角为30°,小宇在山脚的平地F处测量这棵树的高,点C到测角仪EF的水平距离CF=1米,从E处测得树顶部A的仰角为45°,树底部B的仰角为20°,求树AB的高度.
(参考数值:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)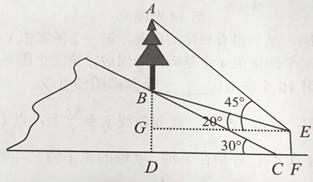
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为正方形ABCD的边BC上一动点(P与B、C不重合),点Q在CD边上,且BP=CQ,连接AP、BQ交于点E,将△BQC沿BQ所在直线对折得到△BQN,延长QN交BA的延长线于点M.
(1)求证:AP⊥BQ;
(2)若AB=3,BP=2PC,求QM的长;
(3)当BP=m,PC=n时,求AM的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com