
【题目】如图,已知A、B两地相距4千米,上午11:00,甲从A地出发步行到B地,11:20乙从B地出发骑自行车到A地,甲乙两人离A地的距离(千米)与甲所用时间(分)之间的关系如图所示,由图中的信息可知,乙到达A地的时间为( )
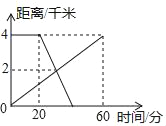
A. 上午11:40 B. 上午11:35 C. 上午11:45 D. 上午11:50
【答案】A
【解析】
根据函数图象,用待定系数法求出甲离A地的距离y与所用的时间x的函数关系式,从而求出甲离A地的距离与所用时间的函数图象与乙离A地的距离与所用时间的函数图象交点坐标,根据待定系数法求出乙离A地的距离y与所用时间x的函数关系式,把y=0代入,即可求出乙从B地到达A地所用的时间,从而得到答案.
设甲离A地的距离y与所用的时间x的函数关系式为:y=kx,
把(60,4)代入得:60k=4,
解得:k=![]() ,
,
即设甲离A地的距离y与所用的时间x的函数关系式为:y=![]() x,
x,
把y=2代入y=![]() x,得
x,得![]() x=2,
x=2,
解得:x=30,
即甲离A地的距离与所用时间的函数图象与乙离A地的距离与所用时间的函数图象交点为(30,2),
设乙离A地的距离y与所用时间x的函数关系式为:y=mx+n,
把(20,4)和(30,2)代入得:![]() ,
,
解得:![]() ,
,
即乙离A地的距离y与所用时间x的函数关系式为:y=-0.2x+8,
当y=0时,-0.2x+8=0,
解得:x=40,
即乙从B地到达A地所用的时间为:40-20=20(分钟),
即乙到达A地的时间为:上午11:40,
故选:A.


科目:初中数学 来源: 题型:
【题目】已知△OAB在直角坐标系中的位置如图,点A在第一象限,点B在x轴正半轴上,OA=OB=6,∠AOB=30°.
(1)求点A、B的坐标;
(2)开口向上的抛物线经过原点O和点B,设其顶点为E,当△OBE为等腰直角三角形时,求抛物线的解析式;
(3)设半径为2的⊙P与直线OA交于M、N两点,已知MN=2 ![]() ,P(m,2)(m>0),求m的值.
,P(m,2)(m>0),求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高节水意识,小申随机统计了自己家7天的用水量,并分析了第3天的用水情况,将得到的数据进行整理后,绘制成如图所示的统计图.(单位:升)
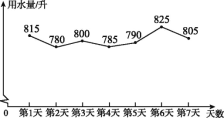
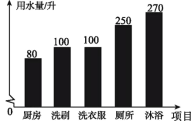
(1)求这7天内小申家每天用水量的平均数和中位数;
(2)求第3天小申家洗衣服的水占这一天总用水量的百分比;
(3)请你根据统计图中的信息,给小申家提出一条全理的节约用水建议,并估算采用你的建议后小申家一个月(按30天计算)的节约用水量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,已知点R(1,0),点K(4,4),直线y=- ![]() x+b过点K , 分别交x轴、y轴于U、V两点,以点R为圆心, RK为半径作⊙R , ⊙R交x轴于A.
x+b过点K , 分别交x轴、y轴于U、V两点,以点R为圆心, RK为半径作⊙R , ⊙R交x轴于A.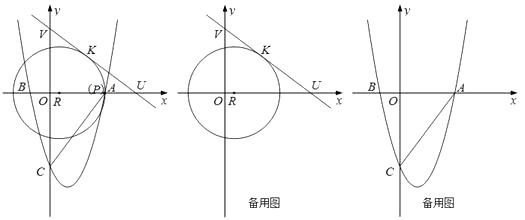
(1)若二次函数的图象经过点A、B(-2,0)、C(0,-8),求二次函数的解析式;
(2)判断直线UV与⊙R的位置关系,并说明理由;
(3)若动点P、Q同时从A点都以相同的速度分别沿AB、AC边运动,当点P运动到B点时,点Q停止运动,这时,在x轴上是否存在点E , 使得以A、E、Q为顶点的三角形是等腰三角形.若存在,请求出E点坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax-2ax-3a(a<0)与x轴交于A、B两点(A在B的左侧),与y轴交于点C,抛物线的对称轴与抛物线交于点P,与直线BC交于点M,且PM= ![]() AB.
AB.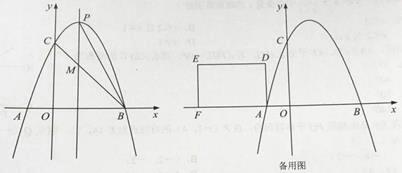
(1)求抛物线的解析式;
(2)点K是x轴正半轴上一点,点A、P关于点K的对称点分别为 ![]() 、
、 ![]() ,连接
,连接 ![]() 、
、 ![]() ,若
,若 ![]()
![]()
![]() ,求点K的坐标;
,求点K的坐标;
(3)矩形ADEF的边AF在x轴负半轴上,边AD在第二象限,AD=2,DE=3.将矩形ADEF沿x轴正方向平移t(t>0)个单位,直线AD、EF分别交抛物线于G、H.问:是否存在实数t,使得以点D、F、G、H为顶点的四边形是平行四边形?若存在,求出t的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,山坡上有一颗树AB,树底部B点到山脚C点的距离BC为6 ![]() 米,山坡的坡角为30°,小宇在山脚的平地F处测量这棵树的高,点C到测角仪EF的水平距离CF=1米,从E处测得树顶部A的仰角为45°,树底部B的仰角为20°,求树AB的高度.
米,山坡的坡角为30°,小宇在山脚的平地F处测量这棵树的高,点C到测角仪EF的水平距离CF=1米,从E处测得树顶部A的仰角为45°,树底部B的仰角为20°,求树AB的高度.
(参考数值:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)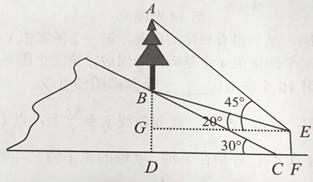
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D为边BC的中点,过点A作射线AE,过点C作CF⊥AE于点F,过点B作BG⊥AE于点G,连接FD并延长,交BG于点H.
(1)求证:DF=DH;
(2)若∠CFD=120°,求证:△DHG为等边三角形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com