
【题目】已知△OAB在直角坐标系中的位置如图,点A在第一象限,点B在x轴正半轴上,OA=OB=6,∠AOB=30°.
(1)求点A、B的坐标;
(2)开口向上的抛物线经过原点O和点B,设其顶点为E,当△OBE为等腰直角三角形时,求抛物线的解析式;
(3)设半径为2的⊙P与直线OA交于M、N两点,已知MN=2 ![]() ,P(m,2)(m>0),求m的值.
,P(m,2)(m>0),求m的值.
【答案】
(1)
解:如图1 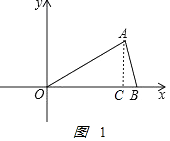 ,
,
作 AC⊥OB于C点,
由OB=OA=6,得B点坐标为(6,0),
由OB=OA=6,∠AOB=30°,得
AC= ![]() OA=3,OC=OAcos∠AOC=
OA=3,OC=OAcos∠AOC= ![]() OA=3
OA=3 ![]() ,
,
∴A点坐标为(3 ![]() ,3);
,3);
(2)
解:如图2 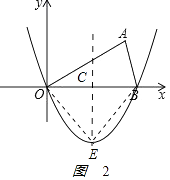 ,
,
由其顶点为E,当△OBE为等腰直角三角形,得
OC=BC=CE= ![]() OB=3,
OB=3,
即E点坐标为(3,﹣3).
设抛物线的解析式为y=a(x﹣3)2﹣3,将B点坐标代入,解得
a= ![]() ,
,
抛物线的解析式为y= ![]() (x﹣3)2﹣3
(x﹣3)2﹣3
化简得y= ![]() x2﹣2x;
x2﹣2x;
(3)
解:如图3 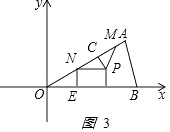 ,
,
PN=2,CN= ![]() ,PC=1,
,PC=1,
∠CNP=∠AOB=30°,
NP∥OB,
NE=2,得ON=4,
由勾股定理,得
OE= ![]() =2
=2 ![]() ,即N(2
,即N(2 ![]() ,2).
,2).
N向右平移2个单位得P(2 ![]() +2,2),
+2,2),
N向左平移2个单位,得P(2 ![]() ﹣2,2),
﹣2,2),
m的值为2 ![]() +2或2
+2或2 ![]() ﹣2.
﹣2.
【解析】(1)根据30°的角所对的直角边是斜边的一半,可得AC的长,再根据锐角三角函数,可得OC,根据点的坐标,可得答案;(2)根据等腰直角三角形,可得E点坐标,再根据待定系数法,可得答案;(3)根据30°的角所对的直角边是斜边的一半,可得∠CNP=30°,再根据勾股定理OE的长,根据点的坐标,可得N点坐标,根据点的左右平移,可得P点坐标.


科目:初中数学 来源: 题型:
【题目】两个三角板ABC,DEF,按如图所示的位置摆放,点B与点D重合,边AB与边DE在同一条直线上(假设图形中所有的点,线都在同一平面内).其中,∠C=∠DEF=90°,∠ABC=∠F=30°,AC=DE=6cm.现固定三角板DEF,将三角板ABC沿射线DE方向平移,当点C落在边EF上时停止运动.设三角板平移的距离为x(cm),两个三角板重叠部分的面积为y(cm2).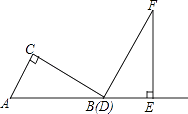
(1)当点C落在边EF上时,x=cm;
(2)求y关于x的函数解析式,并写出自变量x的取值范围;
(3)设边BC的中点为点M,边DF的中点为点N.直接写出在三角板平移过程中,点M与点N之间距离的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B、C、D在⊙O上,DE⊥OA,DF⊥OB,垂足分别为E,F,若∠EDF=50°,则∠C的度数为( ) 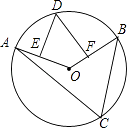
A.40°
B.50°
C.65°
D.130°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家1至6月份的用水量统计如图所示,关于这组数据,下列说法错误的是( ).
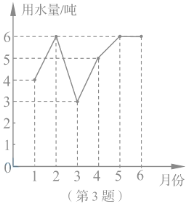
A、众数是6吨 B、平均数是5吨 C、中位数是5吨 D、方差是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一轮船在P处测得灯塔A在正北方向,灯塔B在南偏东30°方向,轮船向正东航行了900m,到达Q处,测得A位于北偏西60°方向,B位于南偏西30°方向.
(1)线段BQ与PQ是否相等?请说明理由;
(2)求A、B间的距离(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某年的日历表,在此日历表上可以用一个矩形圈出3×3个位置的9个数(如3,4,5,10,11,12,17,18,19).若用这样的矩形圈圈这张日历表的9个数,则圈出的9个数的和不可能为下列数中的( )

A. 81 B. 90 C. 108 D. 216
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A、B两地相距4千米,上午11:00,甲从A地出发步行到B地,11:20乙从B地出发骑自行车到A地,甲乙两人离A地的距离(千米)与甲所用时间(分)之间的关系如图所示,由图中的信息可知,乙到达A地的时间为( )
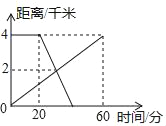
A. 上午11:40 B. 上午11:35 C. 上午11:45 D. 上午11:50
查看答案和解析>>
科目:初中数学 来源: 题型:
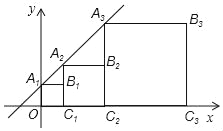
【题目】如图,正方形A1B1C1D1、A2B2C2D2……按照如图所示的方式放置,点A1、A2、A3、…和点C1、C2、C3、…分别在直线y=kx+b(k>0)和x轴上,已知B1(1,1),B2(3,2),B3(7,4)则B2018的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形 ABCD 中,AB=AD,AC=5,∠DAB=∠DCB=90°, 则四边形 ABCD 的面积为( )
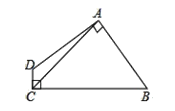
A. 15 B. 14.5 C. 13 D. 12.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com