
����Ŀ���������ǰ�ABC��DEF������ͼ��ʾ��λ�ðڷţ���B���D�غϣ���AB���DE��ͬһ��ֱ���ϣ�����ͼ�������еĵ㣬�߶���ͬһƽ���ڣ������У���C=��DEF=90�㣬��ABC=��F=30�㣬AC=DE=6cm���̶ֹ����ǰ�DEF�������ǰ�ABC������DE����ƽ�ƣ�����C���ڱ�EF��ʱֹͣ�˶��������ǰ�ƽ�Ƶľ���Ϊx��cm�����������ǰ��ص����ֵ����Ϊy��cm2����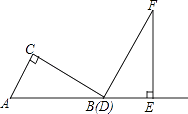
��1������C���ڱ�EF��ʱ��x=cm��
��2����y����x�ĺ�������ʽ����д���Ա���x��ȡֵ��Χ��
��3�����BC���е�Ϊ��M����DF���е�Ϊ��N��ֱ��д�������ǰ�ƽ�ƹ����У���M���N֮��������Сֵ��
���𰸡�
��1��15
��2��
�⣺�ٵ�0��x��6ʱ����ͼ2��ʾ��
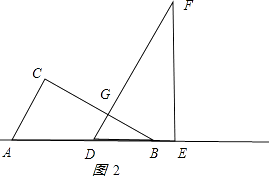 ��
��
��GDB=60�㣬��GBD=30�㣬DB=x����
DG= ![]() x��BG=
x��BG= ![]() x���ص����ֵ����Ϊy=
x���ص����ֵ����Ϊy= ![]() DGBG=
DGBG= ![]() ��
�� ![]() x��
x�� ![]() x=
x= ![]() x2
x2
�ڵ�6��x��12ʱ����ͼ3��ʾ��
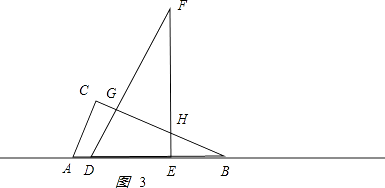 ��
��
BD=x��DG= ![]() x��BG=
x��BG= ![]() x��BE=x��6��EH=
x��BE=x��6��EH= ![]() ��x��6����
��x��6����
�ص����ֵ����Ϊy=S��BDG��S��BEH= ![]() DGBG��
DGBG�� ![]() BEEH��
BEEH��
��y= ![]() ��
�� ![]() x��
x�� ![]() x��
x�� ![]() ��x��6��
��x��6�� ![]() ��x��6��
��x��6��
����y=�� ![]() x2+2
x2+2 ![]() x��6
x��6 ![]() ��
��
�۵�12��x��15ʱ����ͼ4��ʾ��
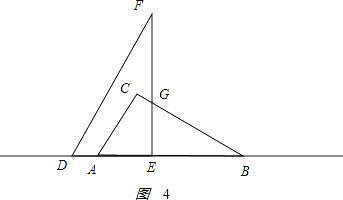 ��
��
AC=6��BC=6 ![]() ��BD=x��BE=��x��6����EG=
��BD=x��BE=��x��6����EG= ![]() ��x��6�����ص����ֵ����Ϊy=S��ABC��S��BEG=
��x��6�����ص����ֵ����Ϊy=S��ABC��S��BEG= ![]() ACBC��
ACBC�� ![]() BEEG��
BEEG��
��y= ![]() ��6��6
��6��6 ![]() ��
�� ![]() ��x��6��
��x��6�� ![]() ��x��6����
��x��6����
����y=18 ![]() ��
�� ![]() ��x2��12x+36��=��
��x2��12x+36��=�� ![]() x2+2
x2+2 ![]() x+12
x+12 ![]() ��
��
����������y= 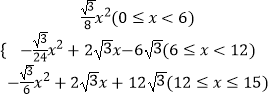
��3��
�⣺��ͼ5��ʾ��NG��DE��G�㣮
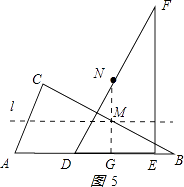 ��
��
��M��NG��ʱMN��̣�
NG�ǡ�DEF����λ�ߣ�
NG= ![]() EF=
EF= ![]() ��
��
MB= ![]() CB=3
CB=3 ![]() ����B=30�㣬
����B=30�㣬
MG= ![]() MB=
MB= ![]() ��
��
MN��С=3 ![]() ��
�� ![]() =
= ![]()
���������⣺��1����ͼ1��ʾ����CG��AB��G�㣮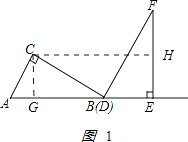 ��
��
��Rt��ABC����AC=6����ABC=30����
BC= ![]() =6
=6 ![]() ��
��
��Rt��BCG��BG=BCcos30��=9��
�ı���CGEH���Σ�
CH=GE=BG+BE=9+6=15cm��
���Դ��ǣ�15��


 ��һ����ͬ���ɽ�����ϵ�д�
��һ����ͬ���ɽ�����ϵ�д� ������Ӧ���ϵ�д�
������Ӧ���ϵ�д� ��ʦ�㾦�ִʾ��ƪϵ�д�
��ʦ�㾦�ִʾ��ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ������1��2��3������n����������������1������1����2������2����3������3���������ƣ���n������n�������������ݵĸ���֮����s����λ����k����s= ����ֻ����k�Ĵ���ʽ��ʾ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ȱ�������OAB��һ��OA��x���ϣ�˫����y= ![]() �ڵ�һ�����ڵ�ͼ��OB�ߵ��е�C�����B�������� ��
�ڵ�һ�����ڵ�ͼ��OB�ߵ��е�C�����B�������� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ����һ����Ϊ2m����Ϊ2n�ij����Σ���ͼ�������ü���ƽ���ֳ��Ŀ�С�����Σ�Ȼ��ͼ�ڵ���״ƴ��һ�������Σ�
��1����ͼ���е���Ӱ���������2�ַ�����ʾ�ɵ�һ����ʽ�����ʽ��
��2����m+2n=7��mn=3�����ã�1���Ľ�����m��2n��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����һЩ���Ϊ1![]() ��С������ǡ�ÿ���������Ϊ1
��С������ǡ�ÿ���������Ϊ1![]() �Ĵ������壬��������ЩС������һ����һ������������������ж���أ�����ѡ������ӽ���һ�߶ȵ��ǣ� ��
�Ĵ������壬��������ЩС������һ����һ������������������ж���أ�����ѡ������ӽ���һ�߶ȵ��ǣ� ��
A. ����ɽ���������ĸ߶� B. ��ˮ��ɭ�ֹ������ָ߶�
C. �������ĸ߶� D. ���ʺ�����и߶�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����a��b�������и�ʽ�У�������ǣ� ��
A.a��3��b��3
B.��a����b
C.��2a����2b
D.![]() a��
a�� ![]() b
b
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڱ߳�Ϊ4������ABCD�У���A=60�㣬M��AD�ߵ��е㣬��N��AB����һ���㣬����AMN��MN���ڵ�ֱ�߷��۵õ���A��MN������A��C�����߶�A��C���ȵ���Сֵ�� �� 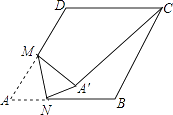
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��OAB��ֱ������ϵ�е�λ����ͼ����A�ڵ�һ���ޣ���B��x���������ϣ�OA=OB=6����AOB=30�㣮
��1�����A��B�����ꣻ
��2���������ϵ������߾���ԭ��O�͵�B�����䶥��ΪE������OBEΪ����ֱ��������ʱ���������ߵĽ���ʽ��
��3����뾶Ϊ2�ġ�P��ֱ��OA����M��N���㣬��֪MN=2 ![]() ��P��m��2����m��0������m��ֵ��
��P��m��2����m��0������m��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com