
四边形ABCD是正方形.
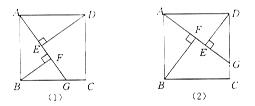
(1)如图1-27(1)所示,点G是BC边上任意一点(不与B,C两点重合),连接AG,作BF⊥AG于点F,DE⊥AG于点E.求证△ABF≌△DAE;
(2)在(1)中,线段EF与AF,BF的等量关系是 ;(不需证明,直接写出结论即可)
(3)如图1-27(2)所示,若点G是CD边上任意一点(不与C,D两点重合),作BF⊥AG于点F,DE⊥AG于点E,那么图中的全等三角形是 ,线段EF与AF,BF的等量关系是 .(不需证明,直接写出结论即可)
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
①如图,是一张很有用的图,你知道∠BOC=∠1+∠2+∠3的奥秘吗?请用你学过的知识予以证明.(可自主添加必要的辅助线)(4+2+2+2= 10分)
10分)
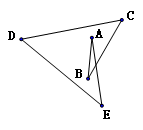

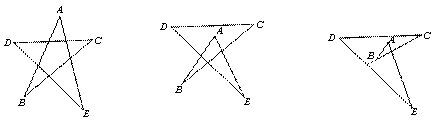
②如图,设x=∠A+∠B+∠C+∠D+∠E.运用①的结论填空:

查看答案和解析>>
科目:初中数学 来源: 题型:
下面几种三角形:
①有两个角为60°的三角形;
②三个外角都相等的三角形;
③一条边上的高也是这条边上的中线的三角形;
④有一个角为60°的等腰三角形.
其中是等边三角形的有 ( )
A.4个 B.3个 C.2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
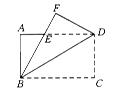
如图1-47所示,把矩形ABCD沿对角线BD折叠,点C落在点F处,若AB=
12 cm,BC=16 cm.
(1)求AE的长;
(2)求重合部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图1—102所示.在ABC中,AC=BC,∠C=90°,AD平分∠CAB交BC于点
D,DE⊥AB于点E.若AB=6 cm,则DEB的周长为 ( )
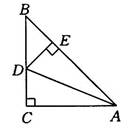
A.12 cm B.8 cm C.6 cm D.4 cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com