
【题目】如图,已知四边形ABCD内接于⊙O,A是 ![]() 的中点,AE⊥AC于A,与⊙O及CB的延长线交于点F、E,且
的中点,AE⊥AC于A,与⊙O及CB的延长线交于点F、E,且 ![]() .
. 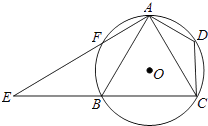
(1)求证:△ADC∽△EBA;
(2)如果AB=8,CD=5,求tan∠CAD的值.
【答案】
(1)证明:∵四边形ABCD内接于⊙O,
∴∠CDA=∠ABE.
∵ ![]() ,
,
∴∠DCA=∠BAE.
∴△ADC∽△EBA
(2)解:∵A是 ![]() 的中点,
的中点,
∴ ![]()
∴AB=AC=8,
∵△ADC∽△EBA,
∴∠CAD=∠AEC, ![]() ,
,
即 ![]() ,
,
∴AE= ![]() ,
,
∴tan∠CAD=tan∠AEC= ![]() =
= ![]() =
= ![]()
【解析】(1)欲证△ADC∽△EBA,只要证明两个角对应相等就可以.可以转化为证明且 ![]() 就可以;(2)A是
就可以;(2)A是 ![]() 的中点,的中点,则AC=AB=8,根据△CAD∽△ABE得到∠CAD=∠AEC,求得AE,根据正切三角函数的定义就可以求出结论.
的中点,的中点,则AC=AB=8,根据△CAD∽△ABE得到∠CAD=∠AEC,求得AE,根据正切三角函数的定义就可以求出结论.
【考点精析】根据题目的已知条件,利用圆周角定理和相似三角形的判定与性质的相关知识可以得到问题的答案,需要掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
【题目】解答题 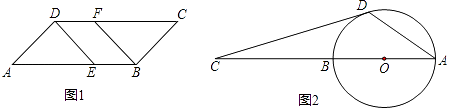
(1)如图1,在平行四边形ABCD中,已知点E在AB上,点F在CD上,且AE=CF.求证:DE=BF;
(2)如图2,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,若∠C=20°,求∠CDA的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①是棱长为a的小正方体,如图②、如图③是由若干这样相同的小正方体摆放而成,按照这样的方法继续摆放,由上而下分别叫第一层、第二层、…、第n层,第n层中小正方体的个数为s(提示:第一层中,s=1;第二层中,s=3),则第n层中,s=________.(用含n的式子表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某一项工程,在工程招标时,接到甲、乙两个工程队的投标书,施工一天,需付甲工程队工程款1.5万元,乙工程队工程款1.1万元,工程领导小组根据甲乙两队的投标书测算,可有三种施工方案:
(1)甲队单独完成这项工程刚好如期完成;
(2)乙队单独完成这项工程要比规定日期多用5天;
(3)若甲、乙两队合作4天,余下的工程由乙队单独也正好如期完成.
在不耽误工期的情况下,你觉得那一种施工方案最节省工程款?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从2017年起,昆明将迎来“高铁时代”,这就意味着今后昆明的市民外出旅行的路程与时间将大大缩短,但也有不少游客根据自己的喜好依然选择乘坐普通列车;已知从昆明到某市的高铁行驶路程是400千米,普通列车的行驶路程是高铁行驶路程的1.3倍,请完成以下问题:(1)普通列车的行驶路程为________千米;(2)若高铁的平均速度(千米/时)是普通列车平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时,求普通列车和高铁的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC⊥BD 于点 , 是 AB 上一点,FD 交 AC 于点 E,∠B 与 ∠D 互余.

(1)试说明:∠A=∠D;
(2)若 AE=1,AC=CD=2.5,求 BD 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=2 ![]() ,以点C为圆心,CB的长为半径画弧,与AB边交于点D,将
,以点C为圆心,CB的长为半径画弧,与AB边交于点D,将 ![]() 绕点D旋转180°后点B与点A恰好重合,则图中阴影部分的面积为
绕点D旋转180°后点B与点A恰好重合,则图中阴影部分的面积为 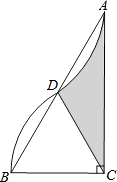
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某储运部紧急调拨一批物资,调进物资共用4小时,调进物资2小时后开始调出物资(调进物资与调出物资的进度均保持不变).储运部库存物资w(吨)与时间t(小时)之间的函数关系如图所示,请问这批物资从开始调进到全部调出需要多长时间?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com