
【题目】如图,在平面直角坐标系xOy中,抛物线y=-x2+bx+c经过点A(3,0)和点B(2,3),过点A的直线与y轴的负半轴相交于点C,且tan∠CAO=![]() .
.
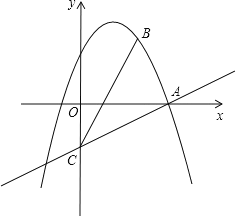
(1)求这条抛物线的表达式及对称轴;
(2)联结AB、BC,求∠ABC的正切值;
(3)若点D在x轴下方的对称轴上,当S△DBC=S△ADC时,求点D的坐标.
【答案】(1)y=-x2+2x+3,对称轴x=1;(2)tan∠ABC=1;(3)点D的坐标为(1,-4).
【解析】
(1)把A(3,0)和点B(2,3)代入y=-x2+bx+c,解方程组即可解决问题;
(2)作BE⊥OA于E.只要证明△AOC≌△BEA,再推出△ABC是等腰直角三角形,即可解决问题;
(3)过点C作CD∥AB交对称轴于D,则S△DBC=S△ADC,先求出直线AB的解析式,再求出直线CD的解析式即可解决问题.
解:(1)把A(3,0)和点B(2,3)代入y=-x2+bx+c得到,
![]() ,解得
,解得![]() ,
,
∴抛物线的表达式为y=-x2+2x+3,
∴对称轴为x=-![]() =1.
=1.
故抛物线的表达式为y=-x2+2x+3,对称轴为x=1;
(2)如图,作BE⊥OA于E.
∵A(3,0),B(2,3),tan∠CAO=![]() ,
,
∴OA=3,OE=2,BE=3,∴AE=1,OC=OA×tan∠CAO=1,
∴BE=OA,AE=OC,
∵∠AEB=∠AOC=90°,
∴△AOC≌△BEA(SAS),
∴AC=AB,∠CAO=∠ABE,
∵∠ABE+∠BAE=90°,
∴∠CAO+∠BAE=90°,
∴∠CAB=90°,
∴△ABC是等腰直角三角形,
∴∠ABC=45°,
∴tan∠ABC=1;
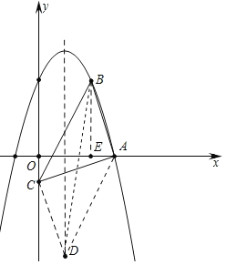
(3)如图,过点C作CD∥AB交对称轴于D,则S△DBC=S△ADC,
设直线AB的解析式为y=kx+b,将A(3,0),B(2,3)代入得,
![]() ,解得
,解得![]() ,∴直线AB的解析式为y=-3x+9.
,∴直线AB的解析式为y=-3x+9.
∵AB∥CD,设直线CD的解析式为y=-3x+m,将点C(0,-1)代入得,m=-1,
∴直线CD的解析式为y=-3x-1,当x=1时,y=-4,
∴点D的坐标为(1,-4).


科目:初中数学 来源: 题型:
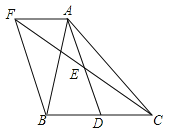
【题目】如图,在![]() 中,
中,![]() 是
是![]() 边上的一点,
边上的一点,![]() 是
是![]() 的中点,过
的中点,过![]() 点作
点作![]() 的平行线交
的平行线交![]() 的延长线于点
的延长线于点![]() ,且
,且![]() ,连接
,连接![]() .
.
(1)求证:![]() 是
是![]() 的中点;
的中点;
(2)如果![]() ,试判断四边形
,试判断四边形![]() 的形状,并证明你的结论.
的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
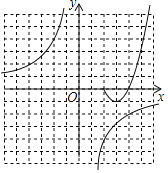
【题目】某数学小组对函数y1=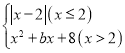 图象和性质进行探究.当x=4时,y1=0.
图象和性质进行探究.当x=4时,y1=0.
(1)当x=5时,求y1的值;
(2)在给出的平面直角坐标系中,补全这个函数的图象,并写出这个函数的一条性质;
(3)进一步探究函数图象并解决问题:已知函数y2=﹣![]() 的图象如图所示,结合函数y1的图象,直接写出不等式y1≥y2的解集.
的图象如图所示,结合函数y1的图象,直接写出不等式y1≥y2的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用各种盛水容器可以制作精致的家用流水景观(如图1).
科学原理:如图2,始终盛满水的圆体水桶水面离地面的高度为H(单位:m),如果在离水面竖直距离为h(单校:cm)的地方开大小合适的小孔,那么从小孔射出水的射程(水流落地点离小孔的水平距离)s(单位:cm)与h的关系为s2=4h(H—h).
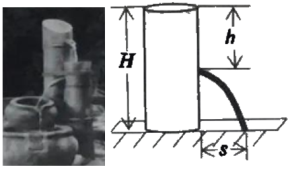
应用思考:现用高度为20cm的圆柱体望料水瓶做相关研究,水瓶直立地面,通过连注水保证它始终盛满水,在离水面竖直距高h cm处开一个小孔.
(1)写出s2与h的关系式;并求出当h为何值时,射程s有最大值,最大射程是多少?
(2)在侧面开两个小孔,这两个小孔离水面的竖直距离分别为a,b,要使两孔射出水的射程相同,求a,b之间的关系式;
(3)如果想通过垫高塑料水瓶,使射出水的最大射程增加16cm,求整高的高度及小孔离水面的竖直距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°.
(1)用尺规在边AB上求作一点P,使PC=PB,并连接PC;(不写作法,保留作图痕迹)
(2)当AC=3,BC=4时,△ACP的周长= ;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术.这本书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等.交易其一,金轻十三两.问金、银一枚各重几何?”.用现代白话文可以这样理解:甲口袋中装有黄金9枚(每枚黄金重量相同),乙口袋中装有白银11枚(每枚白银重量相同),用称分别称这两个口袋的重量,它们的重量相等.若从甲口袋中拿出1枚黄金放入乙口袋中,乙口袋中拿出1枚白银放入甲口袋中,则甲口袋的重量比乙口袋的重量轻了13两(袋子重量忽略不计).问一枚黄金和一枚白银分别重多少两?请根据题意列方程(组)解之.
查看答案和解析>>
科目:初中数学 来源: 题型:
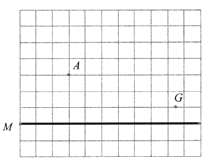
【题目】如图,在每个小正方形的边长为1的网格中,A,M,N均在格点上.在线段![]() 上有一动点B,以
上有一动点B,以![]() 为直角边在
为直角边在![]() 的右侧作等腰直角
的右侧作等腰直角![]() ,使
,使![]() ,
,![]() ,G是一个小正方形边的中点.
,G是一个小正方形边的中点.
(1)当点B的位置满足![]() 时,求此时
时,求此时![]() 的长_______;
的长_______;
(2)请用无刻度的直尺,在如图所示的网格中,画出一个点C,使其满足线段![]() 最短,并简要说明点C的位置是如何找到的(不要求证明)____________.
最短,并简要说明点C的位置是如何找到的(不要求证明)____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系xOy中,直线y=2x+2和直线y=![]() x+2分别交x轴于点A和点B.则下列直线中,与x轴的交点不在线段AB上的直线是( )
x+2分别交x轴于点A和点B.则下列直线中,与x轴的交点不在线段AB上的直线是( )
A.y=x+2B.y=![]() x+2C.y=4x+2D.y=
x+2C.y=4x+2D.y=![]() x+2
x+2
查看答案和解析>>
科目:初中数学 来源: 题型:
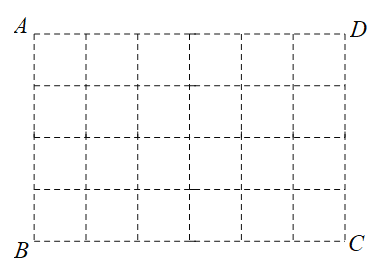
【题目】如图,在6×4的方格纸ABCD中,请按要求画格点线段(端点在格点上),且线段的端点均不与点A,B,C,D重合.
(1)在图1中画格点线段EF,GH各一条,使点E,F,G,H分别落在边AB,BC,CD,DA上,且EF=GH,EF不平行GH;
(2)在图2中画格点线段MN,PQ各一条,使点M,N,P,Q分别落在边AB,BC,CD,DA上,且PQ=![]() MN.
MN.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com