
【题目】已知在平面直角坐标系xOy中,直线y=2x+2和直线y=![]() x+2分别交x轴于点A和点B.则下列直线中,与x轴的交点不在线段AB上的直线是( )
x+2分别交x轴于点A和点B.则下列直线中,与x轴的交点不在线段AB上的直线是( )
A.y=x+2B.y=![]() x+2C.y=4x+2D.y=
x+2C.y=4x+2D.y=![]() x+2
x+2
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
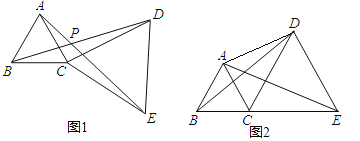
【题目】如图1,△ABC和△DCE都是等边三角形.
探究发现
(1)△BCD与△ACE是否全等?若全等,加以证明;若不全等,请说明理由.
拓展运用
(2)若B、C、E三点不在一条直线上,∠ADC=30°,AD=3,CD=2,求BD的长.
(3)若B、C、E三点在一条直线上(如图2),且△ABC和△DCE的边长分别为1和2,求△ACD的面积及AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,抛物线y=-x2+bx+c经过点A(3,0)和点B(2,3),过点A的直线与y轴的负半轴相交于点C,且tan∠CAO=![]() .
.
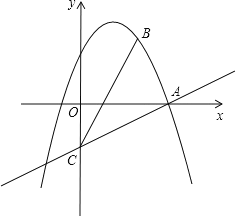
(1)求这条抛物线的表达式及对称轴;
(2)联结AB、BC,求∠ABC的正切值;
(3)若点D在x轴下方的对称轴上,当S△DBC=S△ADC时,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 交x轴于A、B两点,其中点A坐标为
交x轴于A、B两点,其中点A坐标为![]() ,与y轴交于点C,且对称轴在y轴的左侧,抛物线的顶点为P.
,与y轴交于点C,且对称轴在y轴的左侧,抛物线的顶点为P.
(1)当![]() 时,求抛物线的顶点坐标;
时,求抛物线的顶点坐标;
(2)当![]() 时,求b的值;
时,求b的值;
(3)在(1)的条件下,点Q为x轴下方抛物线上任意一点,点D是抛物线对称轴与x轴的交点,直线![]() 、
、![]() 分别交抛物线的对称轴于点M、N.请问
分别交抛物线的对称轴于点M、N.请问![]() 是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果商计划购进甲、乙两种水果进行销售,经了解,甲种水果的进价比乙种水果的进价每千克少4元,且用800元购进甲种水果的数量与用1000元购进乙种水果的数量相同.
(1)求甲、乙两种水果的单价分别是多少元?
(2)该水果商根据该水果店平常的销售情况确定,购进两种水果共200千克,其中甲种水果的数量不超过乙种水果数量的3倍,且购买资金不超过3420元,购回后,水果商决定甲种水果的销售价定为每千克20元,乙种水果的销售价定为每千克25元,则水果商应如何进货,才能获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生对网上在线学习效果的满意度,某校设置了:非常满意、满意、基本满意、不满意四个选项,随机抽查了部分学生,要求每名学生都只选其中的一项,并将抽查结果绘制成如图统计图(不完整).
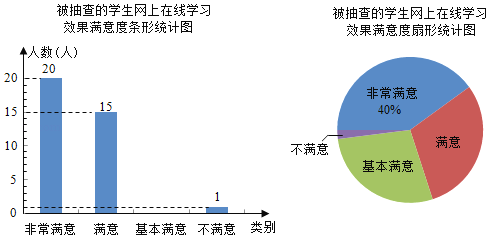
请根据图中信息解答下列问题:
(1)求被抽查的学生人数,并补全条形统计图;(温馨提示:请画在答题卷相对应的图上)
(2)求扇形统计图中表示“满意”的扇形的圆心角度数;
(3)若该校共有1000名学生参与网上在线学习,根据抽查结果,试估计该校对学习效果的满意度是“非常满意”或“满意”的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠BAC=90°,点D在AC上,点E在BA的延长线上,且CD=AE过点A作AF⊥CE,垂足为F,过点D作BC的平行线,交AB于点G,交FA的延长线于点H.
(1)求证∠ACE=∠BAH;
(2)在图中找出与CE相等的线段,并证明;
(3)若GH=![]() DH,求
DH,求![]() 的值(用含
的值(用含![]() 的代数式表示).
的代数式表示).
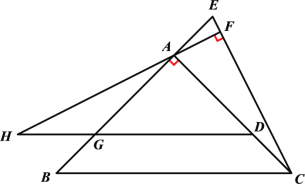
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线![]() x+6与y轴交于点A,与x轴交于点D,直线AB交x轴于点B,将△AOB沿直线AB折叠,点O恰好落在直线AD上的点C处.
x+6与y轴交于点A,与x轴交于点D,直线AB交x轴于点B,将△AOB沿直线AB折叠,点O恰好落在直线AD上的点C处.
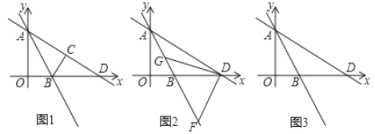
(1)求OB的长;
(2)如图2,F,G是直线AB上的两点,若△DFG是以FG为斜边的等腰直角三角形,求点F的坐标;
(3)如图3,点P是直线AB上一点,点Q是直线AD上一点,且P,Q均在第四象限,点E是x轴上一点,若四边形PQDE为菱形,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
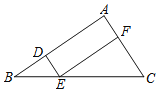
【题目】如图,在△ABC中,点D,E,F分别在AB,BC,AC边上,DE∥AC,EF∥AB.
(1)求证:△BDE∽△EFC.
(2)设![]() ,
,
①若BC=12,求线段BE的长;
②若△EFC的面积是20,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com